题目内容
函数 的零点所在的区间是
的零点所在的区间是
A. | B. | C. | D.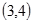 |
C
解析试题分析:首先函数的定义域是 ,且函数在定义域上是连续的。由函数解析式可得
,且函数在定义域上是连续的。由函数解析式可得 ;
; ;
; ,所以由根的存在性定理可以判断出,函数在区间
,所以由根的存在性定理可以判断出,函数在区间 上存在零点。
上存在零点。
考点:本题主要考查根的存在性定理:连续函数在区间 上是否存在零点的问题,由根的存在性定理判断只要
上是否存在零点的问题,由根的存在性定理判断只要 即可。
即可。
点评:本题难度中等,比较注重基础。

练习册系列答案
相关题目
已知函数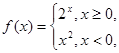 则
则 ( )
( )
| A.16 | B. | C.4 | D.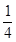 |
已知函数 ,则
,则 等于( )
等于( )
| A.4 | B. | C. | D. |
已知 ,
, ,
, ,则
,则 的大小关系是
的大小关系是
A. | B. |
C.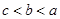 | D. |
若函数 ,则
,则 的值为( )
的值为( )
A. | B. | C. | D. |
设偶函数f(x)的定义域为R,当x 时f(x)是增函数,则f(-2),f(
时f(x)是增函数,则f(-2),f( ),f(-3)的大小关系是( )
),f(-3)的大小关系是( )
A.f( )>f(-3)>f(-2) )>f(-3)>f(-2) | B.f( )>f(-2)>f(-3) )>f(-2)>f(-3) |
C.f( )<f(-3)<f(-2) )<f(-3)<f(-2) | D.f( )<f(-2)<f(-3) )<f(-2)<f(-3) |
已知关于 的二次函数
的二次函数 在区间
在区间 上是单调函数,则
上是单调函数,则 的取值范围是( )
的取值范围是( )
A.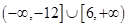 | B. |
C. | D. |
 、
、 、
、 、
、 在同一坐标系中的图象如图所示,则
在同一坐标系中的图象如图所示,则 与1的大小关系为 ( )
与1的大小关系为 ( )




 与
与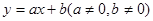 的函数图象只可能是( )
的函数图象只可能是( )