题目内容
已知函数f(x)=ax+lnx(a∈R),
(Ⅰ)若a=-1,求曲线y=f(x)在 处的切线的斜率;
处的切线的斜率;
(Ⅱ)求f(x)的单调区间;
(Ⅲ)设g(x)=2x-2,若存在x1∈(0,+∞),对于任意x2∈[0,1],使f(x1)≥g(x2),求a的范围.
解:(Ⅰ)∵f(x)=ax+lnx,∴ (x>0)
(x>0)
若a=-1,
(Ⅱ)当a≥0,f′(x)>0,∴f(x)在(0,+∞)为增函数
当a<0,令f′(x)>0,∴ ,f′(x)<0,∴
,f′(x)<0,∴ ,
,
综上:a≥0,f(x)的单调增区间为(0,+∞);a<0时,f(x)的单调增区间为(0,- ),单调减区间为(-
),单调减区间为(-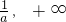 );
);
(Ⅲ)由(Ⅱ)知,当a≥0时,符合题意;
当a<0时,f(x)的单调增区间为(0,- ),单调减区间为(-
),单调减区间为(-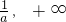 )
)
∴
由题意知,只需满足f(x)max≥g(x)max=g(1)=0,∴ ,
,
∴
综上:
分析:(Ⅰ)求导函数,代入计算,即可求曲线y=f(x)在 处的切线的斜率;
处的切线的斜率;
(Ⅱ)分类讨论,利用导数的正负,可求f(x)的单调区间;
(Ⅲ)分别求出函数的最大值,建立不等式,即可求a的范围.
点评:本题考查导数知识的运用,考查函数的单调性与最值,考查学生的计算能力,属于中档题.
 (x>0)
(x>0)若a=-1,

(Ⅱ)当a≥0,f′(x)>0,∴f(x)在(0,+∞)为增函数
当a<0,令f′(x)>0,∴
 ,f′(x)<0,∴
,f′(x)<0,∴ ,
,综上:a≥0,f(x)的单调增区间为(0,+∞);a<0时,f(x)的单调增区间为(0,-
 ),单调减区间为(-
),单调减区间为(-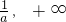 );
);(Ⅲ)由(Ⅱ)知,当a≥0时,符合题意;
当a<0时,f(x)的单调增区间为(0,-
 ),单调减区间为(-
),单调减区间为(-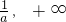 )
)∴

由题意知,只需满足f(x)max≥g(x)max=g(1)=0,∴
 ,
,∴

综上:

分析:(Ⅰ)求导函数,代入计算,即可求曲线y=f(x)在
 处的切线的斜率;
处的切线的斜率;(Ⅱ)分类讨论,利用导数的正负,可求f(x)的单调区间;
(Ⅲ)分别求出函数的最大值,建立不等式,即可求a的范围.
点评:本题考查导数知识的运用,考查函数的单调性与最值,考查学生的计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目