题目内容
设命题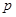 :函数
:函数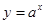 在
在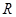 上单调递增;命题
上单调递增;命题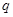 :不等式
:不等式
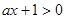 对任意的
对任意的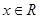 恒成立.若“
恒成立.若“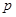 且
且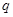 ”为假,“
”为假,“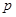 或
或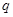 ”为真,求
”为真,求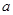 的取值范围.
的取值范围.
【答案】

【解析】解:∵ 在
在 上单调递增 ∴
上单调递增 ∴
又不等式
 对任意的
对任意的 恒成立
恒成立
当 时,不等式可化为
时,不等式可化为 ,符合题意
,符合题意
当 时,
时,
 ∴
∴
∵“ 且
且 ”为假,“
”为假,“ 或
或 ”为真 ∴
”为真 ∴ 、
、 中有且只有一个为真.
中有且只有一个为真.
⑴若“ 真
真 假”,则
假”,则

⑵若“ 假
假 真”,则
真”,则

综上, 的取值范围是
的取值范围是 .
.

练习册系列答案
相关题目
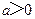 ,设命题
,设命题 :函数
:函数 在
在 上单调递增,命题
上单调递增,命题 :不等式
:不等式 ,对
,对 恒成立,若
恒成立,若 的取值范围
的取值范围 ,设命题
,设命题 :函数
:函数 在
在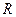 上单调递增;命题
上单调递增;命题 :不等式
:不等式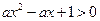 对
对 恒成立。若
恒成立。若 为真命题,
为真命题, 为假命题,求实数
为假命题,求实数 的取值范围。
的取值范围。 ,设命题
,设命题 :函数
:函数 在
在 上单调递增;命题
上单调递增;命题 :不等式
:不等式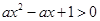 对
对 恒成立。若
恒成立。若 为真命题,
为真命题, 为假命题,求实数
为假命题,求实数 的取值范围。
的取值范围。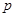 :函数
:函数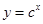 在
在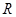 上单调递减
上单调递减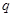 :关于
:关于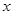 不等式
不等式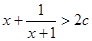 对于
对于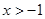 恒成立
恒成立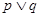 是真命题,
是真命题,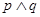 是假命题,求
是假命题,求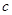 的范围.
的范围.