题目内容
（本小题满分15分）如图，斜三棱柱ABC—A1B1C1中，A1C1⊥BC1，AB⊥AC，AB=3，AC=2，侧棱与底面成60°角．
（1）求证：AC⊥面ABC1；
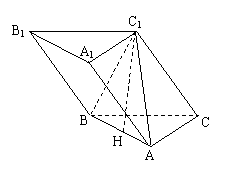（2）求证：C1点在平面ABC上的射影H在直线AB上；
（3）求此三棱柱体积的最小值．
（1）由棱柱性质，可知A1C1//AC，∵A1C1
BC1，
∴ACBC1，又∵ACAB，∴AC平面ABC1
（2）由（1）知AC平面ABC1，又AC
平面ABC，∴平面ABC平面ABC1，
在平面ABC1内，过C1作C1HAB于H，则C1H平面ABC，故点C1在平面ABC上
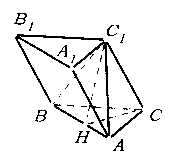的射影H在直线AB上.
（3）连结HC，由（2）知C1H平面ABC， ∴∠C1CH就是侧棱CC1与底面所成的角，
∴∠C1CH=60°，C1H=CH·tan60°=
V棱柱=
∵CAAB，∴CH
，所以棱柱体积最小值3
.
练习册系列答案
相关题目
的单调区间；
，试分别解答以下两小题.
对任意的
恒成立，求实数
的取值范围；
是两个不相等的正数，且
，求证：
．
、
分别为椭圆
：
的 
：
的焦点，
是
。
：
，过点P的动直线
与圆
，
（
且
）。求证：点Q总在某定直线上。
的左、右焦点分别为
、
，过
与椭圆相交于A、B两点。
，且
，求椭圆的离心率；
求
的最大值和最小值。
在定义域内存在区间
，满足
是否为“优美函数”？若是，求出
；若不是，说明理由；
为“优美函数”，求实数
的取值范围．