题目内容
已知直三棱柱ABC-A1B1Cl中，∠BCA=90°，点E、F分别是A1B1、A1C1的中点，若BC=CA=AA1，则BE与AF所成的角的余弦值为________．
分析：连接EF，取BC中点M，连接BE，MF，可得FA与FM成锐角或直角是异面直线BE和AF成角，进而利用余弦定理，可得结论．
解答：连接EF，取BC中点M，连接BE，MF
∵点E、F分别是A1B1、A1C1的中点，∴四边形BMFE平行四边形，
∴MF∥BE，
故FA与FM成锐角或直角是异面直线BE和AF成角．
设BC=CA=C1C=1，点E、F分别是A1B1、A1C1的中点，则AM=
，MF=
，AF=
∴cos∠MFA=
=
即BE与AF所成的角的余弦值为
故答案为：
点评：本题考查空间点、线、面的位置关系及学生的空间想象能力，考查求异面直线所成角，正确作出异面直线所成角是关键．
练习册系列答案
阅读快车系列答案
相关题目
如图，已知直三棱柱ABC-A1B1C1，∠ACB=90°，AC=BC=2，AA1=4．E、F分别是棱CC1、AB中点．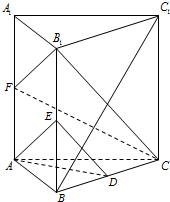
已知直三棱柱ABC-A1B1C1的所有棱长都相等，且D，E，F分别为BC，BB1，AA1的中点．
如图所示，已知直三棱柱ABC-A′B′C′，AC=AB=AA′=2，AC，AB，AA′两两垂直，E，F，H分别是AC，AB，BC的中点，
如图，已知直三棱柱ABC-A1B1C1的侧棱长为2，底面△ABC是等腰直角三角形，且∠ACB=90°，AC=2，D是A A1的中点．
如图，已知直三棱柱ABC-A1B1C1中，AB=AC；M．N．P分别是棱BC．CC1．B1C1的中点．