题目内容
已知数列 与
与 ,若
,若 且对任意正整数
且对任意正整数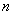 满足
满足 数列
数列 的前
的前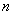 项和
项和 .
.
(I)求数列 的通项公式;
的通项公式;
(II)求数列 的前
的前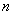 项和
项和
1)因为对任意正整数n满足
所以 是公差为2的等差数列 又因为
是公差为2的等差数列 又因为 所以
所以 (2分)
(2分)
当 时,
时, ; (3分)
; (3分)
当 时,
时, (4分)
(4分)
对 不成立。
不成立。
所以,数列 的通项公式:
的通项公式:  (5分)
(5分)
2)由1)知当 时
时  (6分)
(6分)
当 时
时 (8分)
(8分)
所以,
 (10分)
(10分)
当n=1时仍成立。 (11分)
所以 对任意正整数n成立。 (12分)
对任意正整数n成立。 (12分)

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 满足条件
满足条件 ,则
,则 的最大值为
的最大值为  :
: ,圆
,圆 与圆
与圆 对称,则圆
对称,则圆 B.
B. 
 D.
D. 
 是双曲线E的两个焦点,以线段
是双曲线E的两个焦点,以线段 为直径的圆与双曲线的一个公共点是M,若
为直径的圆与双曲线的一个公共点是M,若 则双曲线E的离心率是
则双曲线E的离心率是 B.
B.  C.
C.  D.
D. 
 ,则目标函数
,则目标函数 的最小值为 .
的最小值为 . 和
和 ,则
,则 =
= B.
B.  C.
C.  D.
D. 
 ,则下列结论正确的是
,则下列结论正确的是 的图像关于直线
的图像关于直线 对称 B.
对称 B.  对称
对称 D.
D.  上为增函数
上为增函数 ,且
,且 ,则
,则 ( )
( ) B、
B、 C、
C、 D、
D、
 是两个命题,若“
是两个命题,若“ ”
” 是假命题,则
是假命题,则  是假命题
是假命题 是真命题 D.
是真命题 D.