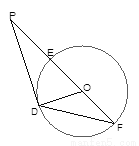
题目内容
设直线的参数方程为
(t为参数),曲线的极坐标方程为ρ=2
cos(θ+
)
(1)求曲线C的直角坐标方程;
(2)求直线l被曲线C所截得的弦长.
|
| 2 |
| π |
| 4 |
(1)求曲线C的直角坐标方程;
(2)求直线l被曲线C所截得的弦长.
(1)∵曲线C的极坐标方程为ρ=2
cos(θ+
),
∴ρ=2cosθ-2sinθ,∴ρ2=2ρcosθ-2ρsinθ,
化为直角坐标方程x2+y2=2x-2y,即为(x-1)2+(y+1)2=2,其圆心C(1,-1),半径r=
.
(2)由直线的参数方程
(t为参数),消去参数t得3x+4y+1=0,
∵圆心C(1,-1)满足直线l的方程3x+4y+1=0,
∴直线l被曲线C所截得的弦长=2r=2
.
| 2 |
| π |
| 4 |
∴ρ=2cosθ-2sinθ,∴ρ2=2ρcosθ-2ρsinθ,
化为直角坐标方程x2+y2=2x-2y,即为(x-1)2+(y+1)2=2,其圆心C(1,-1),半径r=
| 2 |
(2)由直线的参数方程
|
∵圆心C(1,-1)满足直线l的方程3x+4y+1=0,
∴直线l被曲线C所截得的弦长=2r=2
| 2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
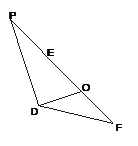 (坐标系与参数方程选做题) 设直线
(坐标系与参数方程选做题) 设直线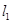 的参数方程为
的参数方程为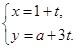 (
(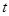 为参数),以坐标原点为极点,x轴为极轴建立极坐标系得另一直线
为参数),以坐标原点为极点,x轴为极轴建立极坐标系得另一直线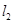 的方程为
的方程为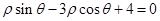 ,
,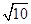 ,则实数
,则实数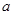 的值为
.
的值为
.