题目内容
设F为双曲线的一个焦点，l为相应的准线，过点F的直线与双曲线一支相交于A、B两点，试推断以线段AB为直径的圆与直线l的位置关系.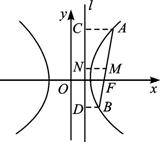
解析：如图，设AB的中点为M（即圆心），过A、B、M分别作准线l的垂线，垂足分别为C、D、N.
设双曲线的离心率为e,据双曲线第二定义，
=e,
∴|AF|=e|AC|,|BF|=e|BD|.
∵MN为梯形ACDB的中位线，
∴|MN|=
（|AC|+|BD|）
=
(|AF|+|BF|)
=
|AB|.
∵e＞1,∴|MN|＜
.
故以AB为直径的圆与直线l相交.
练习册系列答案
相关题目
，P为双曲线上任意一点，F为双曲线的一个焦点，讨论以|PF|为直径的圆与圆x2＋y2=a2的位置关系．
的一个焦点，经过两曲线交点的直线恰过点F，则该双曲线的离心率为 ．
的一个焦点，经过两曲线交点的直线恰过点F，则该双曲线的离心率为 ．
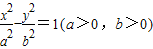的一个焦点，经过两曲线交点的直线恰好过点F，则该双曲线的离心率为（ ）
