题目内容
在f1(x)=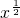 ,f2(x)=x2,f3(x)=2x,f4(x)=
,f2(x)=x2,f3(x)=2x,f4(x)= x四个函数中,x1>x2>1时,能使
x四个函数中,x1>x2>1时,能使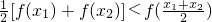 ;成立的函数是
;成立的函数是
- A.f1(x)=
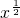
- B.f2(x)=x2
- C.f3(x)=2x
- D.f4(x)=
 x
x
A
分析:因为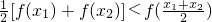 ;表示连接两点A(x1,f(x1)),B (x2,f(x2))的线段的中点纵坐标小于f(x)在曲线AB中点
;表示连接两点A(x1,f(x1)),B (x2,f(x2))的线段的中点纵坐标小于f(x)在曲线AB中点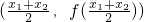 ;的纵坐标,也就是说f(x)的图象“上凸”.所以只需判断哪个函数的图象“上凸”即可.
;的纵坐标,也就是说f(x)的图象“上凸”.所以只需判断哪个函数的图象“上凸”即可.
解答:∵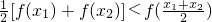 ;表示连接两点A(x1,f(x1)),B (x2,f(x2))的线段的中点纵坐标小于f(x)在曲线AB中点
;表示连接两点A(x1,f(x1)),B (x2,f(x2))的线段的中点纵坐标小于f(x)在曲线AB中点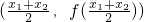 ;的纵坐标,
;的纵坐标,
也就是说f(x)的图象“上凸”.所以只需判断哪个函数的图象“上凸”即可.
由图形可直观得到:B,C,D 的图象都不是上土的,只有f1(x)=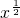 为“上凸”的函数.
为“上凸”的函数.
故选A.
点评:(1)不要忽视条件:x1>x2>1,它表示函数f(x)在(1,+∞)上“上凸”;
(2)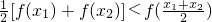 ;表示函数f(x)上凸;
;表示函数f(x)上凸;
(3)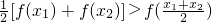 ;表示函数f(x)下凸.
;表示函数f(x)下凸.
分析:因为
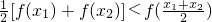 ;表示连接两点A(x1,f(x1)),B (x2,f(x2))的线段的中点纵坐标小于f(x)在曲线AB中点
;表示连接两点A(x1,f(x1)),B (x2,f(x2))的线段的中点纵坐标小于f(x)在曲线AB中点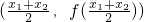 ;的纵坐标,也就是说f(x)的图象“上凸”.所以只需判断哪个函数的图象“上凸”即可.
;的纵坐标,也就是说f(x)的图象“上凸”.所以只需判断哪个函数的图象“上凸”即可.解答:∵
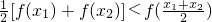 ;表示连接两点A(x1,f(x1)),B (x2,f(x2))的线段的中点纵坐标小于f(x)在曲线AB中点
;表示连接两点A(x1,f(x1)),B (x2,f(x2))的线段的中点纵坐标小于f(x)在曲线AB中点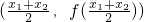 ;的纵坐标,
;的纵坐标,也就是说f(x)的图象“上凸”.所以只需判断哪个函数的图象“上凸”即可.
由图形可直观得到:B,C,D 的图象都不是上土的,只有f1(x)=
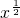 为“上凸”的函数.
为“上凸”的函数.故选A.
点评:(1)不要忽视条件:x1>x2>1,它表示函数f(x)在(1,+∞)上“上凸”;
(2)
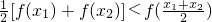 ;表示函数f(x)上凸;
;表示函数f(x)上凸;(3)
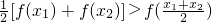 ;表示函数f(x)下凸.
;表示函数f(x)下凸. 
练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
在f1(x)=x
,f2(x)=x2,f3(x)=2x,f4(x)=log
x四个函数中,x1>x2>1时,能使
[f(x1)+f(x2)]<f(
);成立的函数是( )
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| x1+x2 |
| 2 |
A、f1(x)=x
| ||
| B、f2(x)=x2 | ||
| C、f3(x)=2x | ||
D、f4(x)=log
|
 图为函数f1(x)=a1x,f2(x)=a2x,f3(x)=log
图为函数f1(x)=a1x,f2(x)=a2x,f3(x)=log