题目内容
定义在R上的函数f(x)满足f(x+2)=﹣f(x),且当x∈[﹣1,1]时,f(x)=x3.
(1)求f(x)在[1,5]上的表达式;
(2)若A={x|f(x)>a,x∈R},且A≠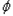 ,求实数a的取值范围.
,求实数a的取值范围.
(1)求f(x)在[1,5]上的表达式;
(2)若A={x|f(x)>a,x∈R},且A≠
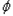 ,求实数a的取值范围.
,求实数a的取值范围.解:(1)由f(x+2)=﹣f(x),
∴f(x+4)=﹣f(x+2)=f(x),
故f(x)的周期为4
(1)当x∈[3,5]时,x﹣4∈(﹣1,1],
∴f(x﹣4)=(x﹣4)3
又T=4,
∴f(x)=f(x﹣4)=(x﹣4)3,
3≤x≤5
当x∈[1,3]时,x﹣2∈[﹣1,1],
∴f(x﹣2)=(x﹣2)3
又f(x)=﹣f(x﹣2)=﹣(x﹣2)3,1≤x≤3,
故f(x)=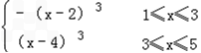
(2)∵f(x)是周期函数,
∴f(x)的值域可以从一个周期来考虑
x∈[1,3]时,f(x)∈(﹣1,1]
x∈[3,5]时,f(x)∈[﹣1,1]
∴f(x)>a,对x∈R有空解,
∴a<1

练习册系列答案
相关题目