题目内容
已知函数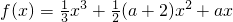 ,x∈R,a∈R.
,x∈R,a∈R.
(Ⅰ)若f′(0)=-2,求函数f(x)的极值;
(Ⅱ)若函数f(x)在(1,2)上单调递增,求a的取值范围.
解:(Ⅰ)∵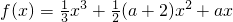 ,∴f′(x)=x2+(a+2)x+a.
,∴f′(x)=x2+(a+2)x+a.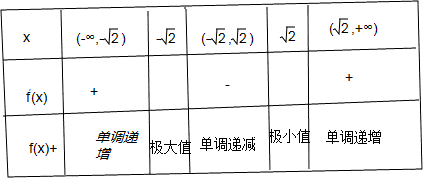
∵f′(0)=-2,∴a=-2.
∴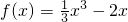 ,f′(x)=x2-2.
,f′(x)=x2-2.
令f′(x)=0,解得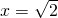 .
.
列表如下:
由表格可以看出:当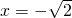 时,f(x)极大值=
时,f(x)极大值=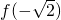 =
= ;
;
当x= 时,f(x)极小值=
时,f(x)极小值=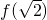 =
=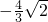 .
.
(Ⅱ)∵函数f(x)在(1,2)上单调递增,
∴f′(x)=x2+(a+2)x+a≥0在区间(1,2)上恒成立.
亦即 在区间(1,2)上恒成立.
在区间(1,2)上恒成立.
令g(x)=- ,则g′(x)=-
,则g′(x)=-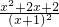 =-
=-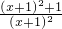 <0,
<0,
∴函数g(x)在x∈(1,2)上为减函数,而函数g(x)在x=1时连续,
∴g(x)<g(1)=- .
.
故a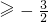 .
.
分析:(Ⅰ)先对函数f(x)求导,再令x=0,即可求出a的值;
(Ⅱ)函数f(x)在(1,2)上单调递增?f′(x)≥0在x∈(1,2)上恒成立? 在区间(1,2)上恒成立?a≥
在区间(1,2)上恒成立?a≥ ,x∈(1,2),解出即可.
,x∈(1,2),解出即可.
点评:利用导数求函数的单调区间、极值、恒成立问题是最有效的方法之一,必须熟练掌握.
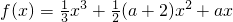 ,∴f′(x)=x2+(a+2)x+a.
,∴f′(x)=x2+(a+2)x+a.
∵f′(0)=-2,∴a=-2.
∴
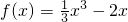 ,f′(x)=x2-2.
,f′(x)=x2-2.令f′(x)=0,解得
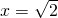 .
.列表如下:
由表格可以看出:当
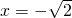 时,f(x)极大值=
时,f(x)极大值=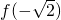 =
= ;
;当x=
 时,f(x)极小值=
时,f(x)极小值=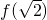 =
=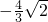 .
.(Ⅱ)∵函数f(x)在(1,2)上单调递增,
∴f′(x)=x2+(a+2)x+a≥0在区间(1,2)上恒成立.
亦即
 在区间(1,2)上恒成立.
在区间(1,2)上恒成立.令g(x)=-
 ,则g′(x)=-
,则g′(x)=-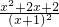 =-
=-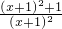 <0,
<0,∴函数g(x)在x∈(1,2)上为减函数,而函数g(x)在x=1时连续,
∴g(x)<g(1)=-
 .
.故a
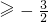 .
.分析:(Ⅰ)先对函数f(x)求导,再令x=0,即可求出a的值;
(Ⅱ)函数f(x)在(1,2)上单调递增?f′(x)≥0在x∈(1,2)上恒成立?
 在区间(1,2)上恒成立?a≥
在区间(1,2)上恒成立?a≥ ,x∈(1,2),解出即可.
,x∈(1,2),解出即可.点评:利用导数求函数的单调区间、极值、恒成立问题是最有效的方法之一,必须熟练掌握.

练习册系列答案
相关题目
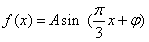 ,x∈R,A>0,
,x∈R,A>0,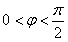 。y=f(x)部分图象如图所示,P、Q分别为该图象的最高点和最低点,点P的坐标为(1,A)。
。y=f(x)部分图象如图所示,P、Q分别为该图象的最高点和最低点,点P的坐标为(1,A)。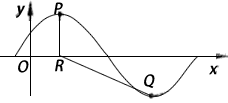
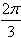 ,求A的值。
,求A的值。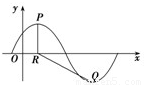 已知函数
已知函数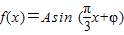 ,x∈R,A>0,
,x∈R,A>0,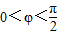 .y=f(x)的部分图象,如图所示,P、Q分别为该图象的最高点和最低点,点P的坐标为(1,A).
.y=f(x)的部分图象,如图所示,P、Q分别为该图象的最高点和最低点,点P的坐标为(1,A).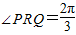 ,求A的值.
,求A的值.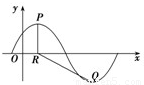 已知函数
已知函数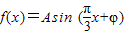 ,x∈R,A>0,
,x∈R,A>0,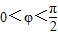 .y=f(x)的部分图象,如图所示,P、Q分别为该图象的最高点和最低点,点P的坐标为(1,A).
.y=f(x)的部分图象,如图所示,P、Q分别为该图象的最高点和最低点,点P的坐标为(1,A).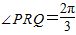 ,求A的值.
,求A的值.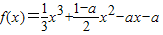 ,x∈R其中a>0.
,x∈R其中a>0. 已知函数
已知函数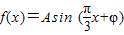 ,x∈R,A>0,
,x∈R,A>0,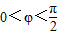 .y=f(x)的部分图象,如图所示,P、Q分别为该图象的最高点和最低点,点P的坐标为(1,A).
.y=f(x)的部分图象,如图所示,P、Q分别为该图象的最高点和最低点,点P的坐标为(1,A).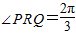 ,求A的值.
,求A的值.