题目内容
三棱锥A-BCD中，AC⊥BD，E、F、G、H分别是AB、BC、CD、DA的中点，则四边形EFGH是（ ）
分析：结合图形，由三角形的中位线定理可得EF∥AC，GH∥AC且EF=
AC，GH=
AC，由平行四边形的定义可得四边形EFGH是平行四边形，再由邻边垂直得到四边形EFGH是矩形．
| 1 |
| 2 |
| 1 |
| 2 |
解答：解：如图所示：∵EF∥AC，GH∥AC且EF=
AC，GH=
AC
∴四边形EFGH是平行四边形
又∵AC⊥BD，∴EF⊥FG
∴四边形EFGH是矩形．
故选B．
| 1 |
| 2 |
| 1 |
| 2 |
∴四边形EFGH是平行四边形
又∵AC⊥BD，∴EF⊥FG
∴四边形EFGH是矩形．
故选B．
点评：本题主要考查棱锥的结构特征，主要涉及了线段的中点，中位线定理，构成平面图形，研究平面图形的形状．
练习册系列答案
字词句篇与同步作文达标系列答案
相关题目
如图，在三棱锥A-BCD中，E、F、G、H分别是边AB、BC、CD、DA的中点．
如图，在三棱锥A-BCD中，AD⊥平面ABC，∠BAC=120°，且AB=AC=AD=2，点E在BC上，且AE⊥AC．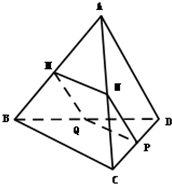
如图，在三棱锥A-BCD中，平行于BC的平面MNPQ分别交AB、AC、CD、BD于M、N、P、Q四点，且MN=PQ．