题目内容
已知函数f(x)=ex-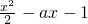 ,(其中a∈R.无理数e=2.71828…)
,(其中a∈R.无理数e=2.71828…)
(Ⅰ)若a=- 时,求曲线y=f(x)在点(1,f(1))处的切线方程;
时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)当x 时,若关于x的不等式f(x)≥0恒成立,试求a的最大值.
时,若关于x的不等式f(x)≥0恒成立,试求a的最大值.
解:(Ⅰ)a=- 时,函数f(x)=ex-
时,函数f(x)=ex-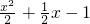 ,求导数可得f′(x)=ex-x+
,求导数可得f′(x)=ex-x+
∴f′(1)=e- ,f(1)=e-1
,f(1)=e-1
∴曲线y=f(x)在点(1,f(1))处的切线方程为y-(e-1)=(e- )(x-1),即(e-
)(x-1),即(e- )x-y-
)x-y- =0;
=0;
(Ⅱ)由f(x)≥0得ax≤ex- x2-1,因为x
x2-1,因为x ,所以a≤
,所以a≤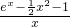 .
.
令g(x)=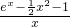 ,则g′(x)=
,则g′(x)=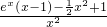 .
.
令h(x)=ex(x-1)- x2+1,所以h′(x)=x(ex-1).
x2+1,所以h′(x)=x(ex-1).
因为x ,所以h′(x)>0,所以h(x)在[
,所以h′(x)>0,所以h(x)在[ ,+∞)上单调增
,+∞)上单调增
所以h(x)≥h( )=
)= -
-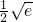 >0
>0
所以g′(x)>0
∴g(x)在[ ,+∞)上单调增
,+∞)上单调增
∴g(x)≥g( )=2
)=2 -
-
∴a≤2 -
-
∴a的最大值为2 -
- .
.
分析:(Ⅰ)求导数,求得切线的斜率,再利用点斜式,可得切线方程;
(Ⅱ)由f(x)≥0,分离参数可得a≤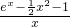 ,确定右边所对应函数的单调性,求出其最小值,即可求得结论.
,确定右边所对应函数的单调性,求出其最小值,即可求得结论.
点评:本题考查导数知识的运用,考查导数的几何意义,考查函数的单调性与最值,考查恒成立问题,正确构建函数是关键.
 时,函数f(x)=ex-
时,函数f(x)=ex-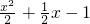 ,求导数可得f′(x)=ex-x+
,求导数可得f′(x)=ex-x+
∴f′(1)=e-
 ,f(1)=e-1
,f(1)=e-1∴曲线y=f(x)在点(1,f(1))处的切线方程为y-(e-1)=(e-
 )(x-1),即(e-
)(x-1),即(e- )x-y-
)x-y- =0;
=0;(Ⅱ)由f(x)≥0得ax≤ex-
 x2-1,因为x
x2-1,因为x ,所以a≤
,所以a≤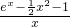 .
.令g(x)=
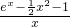 ,则g′(x)=
,则g′(x)=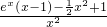 .
.令h(x)=ex(x-1)-
 x2+1,所以h′(x)=x(ex-1).
x2+1,所以h′(x)=x(ex-1).因为x
 ,所以h′(x)>0,所以h(x)在[
,所以h′(x)>0,所以h(x)在[ ,+∞)上单调增
,+∞)上单调增所以h(x)≥h(
 )=
)= -
-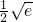 >0
>0所以g′(x)>0
∴g(x)在[
 ,+∞)上单调增
,+∞)上单调增∴g(x)≥g(
 )=2
)=2 -
-
∴a≤2
 -
-
∴a的最大值为2
 -
- .
.分析:(Ⅰ)求导数,求得切线的斜率,再利用点斜式,可得切线方程;
(Ⅱ)由f(x)≥0,分离参数可得a≤
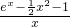 ,确定右边所对应函数的单调性,求出其最小值,即可求得结论.
,确定右边所对应函数的单调性,求出其最小值,即可求得结论.点评:本题考查导数知识的运用,考查导数的几何意义,考查函数的单调性与最值,考查恒成立问题,正确构建函数是关键.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目