题目内容
定义在(-1,1)上的奇函数f(x)=
,则常数m=______,n=______.
| x+m |
| x2+nx+1 |
因为函数f(x)是定义在(-1,1)上的奇函数,所以必定有f(0)=
=0?m=0,
此时f(x)=
,
函数f(x)是定义在(-1,1)上的奇函数得到f(-1)=-f(1),
即:f(-1)=
=-f(1)=-
?n=0.
故答案为:m=0,n=0.
| m |
| 1 |
此时f(x)=
| x |
| x2+nx+1 |
函数f(x)是定义在(-1,1)上的奇函数得到f(-1)=-f(1),
即:f(-1)=
| -1 |
| 1-n+1 |
| 1 |
| 1+n+1 |
故答案为:m=0,n=0.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 是定义在(-1,1)的奇函数,且f(
是定义在(-1,1)的奇函数,且f( )=
)= .
.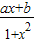 是定义在(-1,1)的奇函数,且f(
是定义在(-1,1)的奇函数,且f( )=
)= .
.