题目内容
设函数 ,
,(1)求证:不论a为何实数f(x)总为增函数;
(2)确定a的值,使f(x)为奇函数及此时f(x)的值域.
【答案】分析:(1)∵f(x)的定义域为R,任设x1<x2,化简f(x1)-f(x2)到因式乘积的形式,判断符号,得出结论.
(2)由f(-x)=-f(x),解出a的值,进而得到函数的解析式: .
.
由 2x+1>1,可得函数的值域.
解答:解:(1)∵f(x)的定义域为R,设 x1<x2,
则 =
= ,
,
∵x1<x2,∴ ,
,
∴f(x1)-f(x2)<0,
即f(x1)<f(x2),所以不论a为何实数f(x)总为增函数.
(2)∵f(x)为奇函数,∴f(-x)=-f(x),
即 ,
,
解得:a=1.∴ .
.
∵2x+1>1,∴ ,
,
∴ ,∴
,∴
所以f(x)的值域为(-1,1).
点评:本题考查证明函数的单调性的方法、步骤,利用奇函数的定义求待定系数的值,及求函数的值域.
(2)由f(-x)=-f(x),解出a的值,进而得到函数的解析式:
 .
.由 2x+1>1,可得函数的值域.
解答:解:(1)∵f(x)的定义域为R,设 x1<x2,
则
 =
= ,
,∵x1<x2,∴
 ,
,∴f(x1)-f(x2)<0,
即f(x1)<f(x2),所以不论a为何实数f(x)总为增函数.
(2)∵f(x)为奇函数,∴f(-x)=-f(x),
即
 ,
,解得:a=1.∴
 .
.∵2x+1>1,∴
 ,
,∴
 ,∴
,∴
所以f(x)的值域为(-1,1).
点评:本题考查证明函数的单调性的方法、步骤,利用奇函数的定义求待定系数的值,及求函数的值域.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
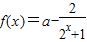 ,
,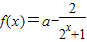 ,
,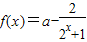 ,
,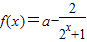 ,
,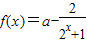 ,
,