Question

设A，B，C，D是不共面的四个点，P，Q，S，R为AC，BC，DB，DA的中点，若AB=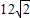，CD=，且四边形PQRS的面积为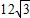，则异面直线AB与CD所成的角等于     ．

Answer 1

【答案】分析：将AB平移到SR，将DC平移到SQ，根据异面直线所成角的定义可知∠SQP为异面直线AB与CD所成的角，最后根据平行四边形的面积公式S=SQ•QP•cos∠SQP求出此角即可．
解答：解：∵SR∥AB，SQ∥DC
∴∠SQP为异面直线AB与CD所成的角
SQ=，QP=
根据平行四边形的面积公式S=SQ•QP•cos∠SQP=2•cos∠SQP=，
解得：cos∠SQP=
∴∠SQP=45°
故答案为：45°
点评：本小题主要考查异面直线所成的角、异面直线所成的角的求法，以及平行四边形的面积等有关知识，考查空间想象能力、运算能力和推理论证能力，考查转化思想，属于基础题．