题目内容
已知a和b是任意非零实数.
(1)求![]() 的最小值.
的最小值.
(2)若不等式|2a+b|+|2a-b|≥|a|(|2+x|+|2-x|)恒成立,求实数x的取值范围.
(1)∵|2a+b|+|2a-b|≥|2a+b+2a-b|=4|a|对于任意非零实数a和b恒成立,
当且仅当(2a+b)(2a-b)≥0时取等号.
∴![]() 的最小值等于4.
的最小值等于4.
(2)∵|2+x|+|2-x|≤![]() 恒成立.
恒成立.
故|2+x|+|2-x|不大于![]() 的最小值.
的最小值.
由(1)可知![]() 的最小值等于4.
的最小值等于4.
实数x的取值范围即为不等式|2+x|+|2-x|≤4的解集.
![]() 解不等式得{x|-2≤x≤2}.
解不等式得{x|-2≤x≤2}.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
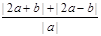 的最小值.
的最小值.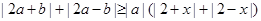 恒成立,求实数x的取值范围.
恒成立,求实数x的取值范围.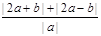 的最小值。
的最小值。 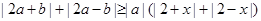 恒成立,求实数x的取值范围.
恒成立,求实数x的取值范围.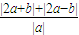 的最小值.
的最小值.