题目内容
试用两种方法证明：
（1）
；
（2）
．
方法一：用组合数的公式证明，方法二：用数学归纳法证明
解析试题分析：（1）证明：方法1 由
令
，得. 3分
方法2 数学归纳法
①当
时，显然成立；
②假设当
时，
，
则当
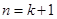时，由
所以，
由①②，等式对于任意
恒成立.
7分
方法3 含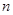
个元素的集合的子集个数按两种方式计算可证
（方法1给4分，其他方法6分）
（2）方法1
先证
. 
，（注意
）
，
所以
。 9分
所以
11分
方法2 由
，
两边求导，得
， 14分
令，得
. 15分
考点：本题考查了组合数的性质及数学归纳法等的运用
点评：数学归纳法是一种证明与正整数n有关的数学命题的重要方法，另外关于组合数的等式常常利用组合数的性质证明
练习册系列答案
相关题目
；
．