题目内容
(文)(本题满分12分)已知圆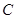 和
和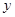 轴相切,圆心在直线
轴相切,圆心在直线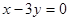 上,且被直线
上,且被直线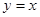 截得的弦长为
截得的弦长为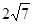
 ,求圆
,求圆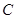 的标准方程。
的标准方程。
【答案】
 或
或
【解析】
试题分析:(文)解:设所求圆方程为 ,
,
由圆心在直线 上
上
则圆心为 ,半径为
,半径为 ,
,
则 而
而 ,则
,则
 或
或
考点:本试题考查了圆的方程的求解。
点评:解决该试题的关键是求解圆心坐标和圆的半径。那么要充分利用直线与圆相交时的性质,圆心距和弦长,以及圆的半径的勾股定理来求解,同时注意圆与坐标轴相切意味着圆心的一个坐标确定了。属于中档题。

练习册系列答案
相关题目
 和
和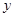 轴相切,圆心在直线
轴相切,圆心在直线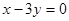 上,且被直线
上,且被直线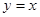 截得的弦长为
截得的弦长为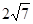
 ,求圆
,求圆 :3x+4y﹣5=0,圆O:x2+y2=4.
:3x+4y﹣5=0,圆O:x2+y2=4. 垂直,
垂直, :3x+4y﹣5=0,圆O:x2+y2=4.
:3x+4y﹣5=0,圆O:x2+y2=4. 垂直,
垂直,