题目内容
设{an}是等差数列,{bn}是各项都为正数的等比数列,且a1=b1=1,a3+b5=19,a5+b3=9,则数列{anbn}的前n项和Sn=________.
(n-1)•2n+1
分析:先根据等差数列、等比数列的通项,结合条件,可求数列{an},{bn}的通项公式,这样就可以利用错位相消法,求出数列{anbn}的前n项和.
解答:设{an}的公差为d,{bn}的公比为q,则由已知条件得
①×2-②:2q4-q2-28=0,∴q2=4
∵q>0,∴q=2
代入②可得:d=1
∴an=n,bn=2n-1
令cn=anbn,则cn=n×2n-1
∴S=1+2×2+…+n×2n-1①
①×2:2S=1×2+2×22+…+n×2n②
①-②:-S=1+2+…+2n-1-n×2n,
∴-S=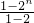 -n×2n,
-n×2n,
∴S=(n-1)•2n+1
故答案为:(n-1)•2n+1
点评:等差数列、等比数列通项的求解通常运用基本量法,求数列的和,一定要弄清数列通项的特征,从而选用适当的方法.
分析:先根据等差数列、等比数列的通项,结合条件,可求数列{an},{bn}的通项公式,这样就可以利用错位相消法,求出数列{anbn}的前n项和.
解答:设{an}的公差为d,{bn}的公比为q,则由已知条件得

①×2-②:2q4-q2-28=0,∴q2=4
∵q>0,∴q=2
代入②可得:d=1
∴an=n,bn=2n-1
令cn=anbn,则cn=n×2n-1
∴S=1+2×2+…+n×2n-1①
①×2:2S=1×2+2×22+…+n×2n②
①-②:-S=1+2+…+2n-1-n×2n,
∴-S=
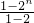 -n×2n,
-n×2n,∴S=(n-1)•2n+1
故答案为:(n-1)•2n+1
点评:等差数列、等比数列通项的求解通常运用基本量法,求数列的和,一定要弄清数列通项的特征,从而选用适当的方法.

练习册系列答案
相关题目
设{an}是等差数列,a1+a3+a5=9,a6=9.则这个数列的前6项和等于( )
| A、12 | B、24 | C、36 | D、48 |