题目内容
三棱锥V-ABC中,AB=AC=10,BC=12,各侧面与底面所成的二面角都是45°,则棱锥的侧面积是
48
| 2 |
48
,高是| 2 |
3
3
.分析:取BC中点M,连接AM,由AB=AC=10,知AM垂直于BC,AM=8,求出S△ABC,利用由各侧面与底面成的二面角都是45°,二面角θ,cosθ=
,求出侧面积;设VP垂直于面ABC于P,由各侧面与底面成的二面角都是45°,知P为△ABC内心,设半径为R,由△ABC的面积求出R=3,由此能求出棱柱的高.
| S△ABC |
| S侧 |
解答: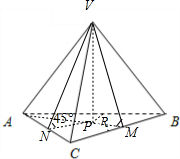 a或者2a
a或者2a
解:取BC中点M,连接AM,
∵AB=AC=10,
∴AM垂直于BC,AM=8,
S△ABC=
×BC×AM=48,
由各侧面与底面成的二面角都是45°,
设二面角θ,cosθ=
,S侧=
=
=48
设VP垂直于面ABC于P,
∵各侧面与底面成的二面角都是45°,
即P为△ABC内心,设半径为R,
则S△ABC=
×(BC+AB+AC)R=16R=48,
R=3,
∴VP=R•tan45°=3.
棱锥的高:3.
故答案为:48
;3.
 a或者2a
a或者2a解:取BC中点M,连接AM,
∵AB=AC=10,
∴AM垂直于BC,AM=8,
S△ABC=
| 1 |
| 2 |
由各侧面与底面成的二面角都是45°,
设二面角θ,cosθ=
| S△ABC |
| S侧 |
| S△ABC |
| cosθ |
| 48 | ||||
|
| 2 |
设VP垂直于面ABC于P,
∵各侧面与底面成的二面角都是45°,
即P为△ABC内心,设半径为R,
则S△ABC=
| 1 |
| 2 |
R=3,
∴VP=R•tan45°=3.
棱锥的高:3.
故答案为:48
| 2 |
点评:本题考查与二面角有关的立体几何综合题,解题时要认真审题,仔细解答,注意三角形面积公式的合理运用.

练习册系列答案
相关题目
 15、如图,三棱锥V-ABC中,VA⊥底面ABC,∠ABC=90°.
15、如图,三棱锥V-ABC中,VA⊥底面ABC,∠ABC=90°.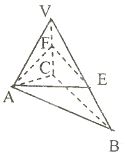 如图所示,侧棱长为
如图所示,侧棱长为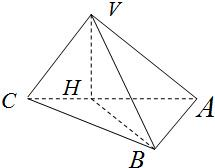 在三棱锥V-ABC中,底面△ABC是以∠ABC为直角的等腰三角形.又V在底面ABC上的射影H在线段AC上且靠近点C,AC=4,
在三棱锥V-ABC中,底面△ABC是以∠ABC为直角的等腰三角形.又V在底面ABC上的射影H在线段AC上且靠近点C,AC=4,