题目内容
如图的程序可产生一系列随机数,其工作原理如下:
①从集合D中随机抽取1个数作为自变量x输入;
②从函数f(x)与g(x)中随机选择一个作为H(x)进行计算;
③输出函数值y.
若D={1,2,3,4,5},f(x)=3x+1,g(x)=x2,
(1)求y=4的概率;
(2)将程序运行4次,求恰好有2次的输出结果是奇数的概率.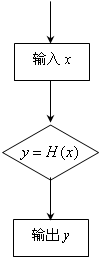
①从集合D中随机抽取1个数作为自变量x输入;
②从函数f(x)与g(x)中随机选择一个作为H(x)进行计算;
③输出函数值y.
若D={1,2,3,4,5},f(x)=3x+1,g(x)=x2,
(1)求y=4的概率;
(2)将程序运行4次,求恰好有2次的输出结果是奇数的概率.

(1)输出4包括2个互斥事件,分别是:以2为自变量,H(x)是g(x)=x2; 以1为自变量,H(x)是f(x)=3x+1,
故所求概率P=
×
+
×
=
;…(6分)
(2)将程序运行一次,输出的结果是奇数包括1,7,9,13,25这5种情况,
故运行一次输出奇数的概率是P=
×
+
×
+
×
+
×
+
×
=
,…(10分)
由独立重复试验的概率计算公式得P4(2)=
•(
)2•(1-
)2=
. …(12分)
故所求概率P=
| 1 |
| 5 |
| 1 |
| 2 |
| 1 |
| 5 |
| 1 |
| 2 |
| 1 |
| 5 |
(2)将程序运行一次,输出的结果是奇数包括1,7,9,13,25这5种情况,
故运行一次输出奇数的概率是P=
| 1 |
| 5 |
| 1 |
| 2 |
| 1 |
| 5 |
| 1 |
| 2 |
| 1 |
| 5 |
| 1 |
| 2 |
| 1 |
| 5 |
| 1 |
| 2 |
| 1 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
由独立重复试验的概率计算公式得P4(2)=
| C | 24 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 8 |

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
 如图的程序可产生一系列随机数,其工作原理如下:
如图的程序可产生一系列随机数,其工作原理如下: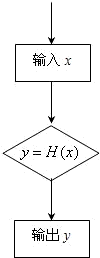 如图的程序可产生一系列随机数,其工作原理如下:
如图的程序可产生一系列随机数,其工作原理如下: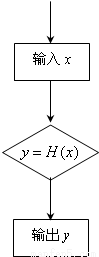 如图的程序可产生一系列随机数,其工作原理如下:
如图的程序可产生一系列随机数,其工作原理如下: