题目内容
已知函数f(x)=lnx-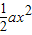 -2x,a∈R.
-2x,a∈R.(1)若f(x)在x=1处的切线与直线x+y=0垂直,求a的值.
(2)若f(x)存在单调递减区间,求a的取值范围.
【答案】分析:(1)求出函数的导数,利用导数的几何意义求切线斜率即可.(2)若f(x)存在单调递减区间,则f'(x)<0有解.
解答:解:函数的定义域为{x|x>0}.
(1)因为f(x)在x=1处的切线与直线x+y=0垂直,所以f(x)在x=1处的切线斜率k=1,
因为f(x)=lnx-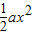 -2x,所以
-2x,所以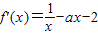 ,
,
则f(x)在x=1处的切线斜率k=f'(1)=1-a-2=1,解得a=-2.
(2)若f(x)存在单调递减区间,则f'(x)<<0有解,则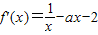 <0.
<0.
即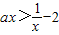 ,在x>0时成立,所以
,在x>0时成立,所以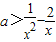 成立即可.
成立即可.
由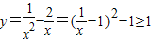 得,a>1.
得,a>1.
故a的取值范围a>1.
点评:本题主要考查导数基本运算以及导数的几何意义,以及函数的单调性与导数之间的关系.
解答:解:函数的定义域为{x|x>0}.
(1)因为f(x)在x=1处的切线与直线x+y=0垂直,所以f(x)在x=1处的切线斜率k=1,
因为f(x)=lnx-
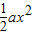 -2x,所以
-2x,所以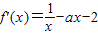 ,
,则f(x)在x=1处的切线斜率k=f'(1)=1-a-2=1,解得a=-2.
(2)若f(x)存在单调递减区间,则f'(x)<<0有解,则
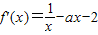 <0.
<0.即
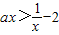 ,在x>0时成立,所以
,在x>0时成立,所以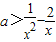 成立即可.
成立即可.由
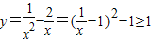 得,a>1.
得,a>1.故a的取值范围a>1.
点评:本题主要考查导数基本运算以及导数的几何意义,以及函数的单调性与导数之间的关系.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案
相关题目