题目内容
已知函数
(1)试判断f(x)的单调性,并说明理由;
(2)若 恒成立,求实数k的取值范围;
恒成立,求实数k的取值范围;
(3)求证:[(n+1)!]2>(n+1)•en-2,(n∈N*).
(1)解:求导函数,可得 =
=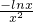
∵x≥1,∴lnx≥0,∴f′(x)≤0,
∴函数f(x)在[1,+∞)上单调减
∴函数f(x)的单调减区间是[1,+∞).
(2)解:不等式 ,即为
,即为 ,记
,记 ,
,
所以 ,
,
令h(x)=x-lnx,则 ,
,
∵x≥1,∴h′(x)≥0.
∴h(x)在[1,+∞)上单调递增,∴[h(x)]min=h(1)=1>0,
从而g′(x)>0
故g(x)在[1,+∞)上也单调递增,
∴[g(x)]min=g(1)=2,所以k≤2
(3)证明:由(2)知: 恒成立,即
恒成立,即 ,
,
令x=n(n+1),则 ,
,
所以 ,
, ,
, ,…,
,…, .
.
叠加得:ln[1×22×32×…×n2×(n+1)]=
则1×22×32×…×n2×(n+1)>en-2,
所以[(n+1)!]2>(n+1)•en-2,(n∈N*).
分析:(1)求导函数,根据函数的定义域,即可确定函数的单调性;
(2)如果当x≥1时,不等式 恒成立,把k分离出来,再利用导数法确定函数的单调性,再求出函数最值即可;
恒成立,把k分离出来,再利用导数法确定函数的单调性,再求出函数最值即可;
(3)由(2)可得 ,令x=n(n+1),则
,令x=n(n+1),则 ,写出n个式子,叠加即可证明结论.
,写出n个式子,叠加即可证明结论.
点评:本题考查应用导数研究函数的极值最值问题,考查不等式的证明,有关恒成立的问题一般采取分离参数,转化为求函数的最值问题,体现了转化的思想方法.
 =
=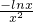
∵x≥1,∴lnx≥0,∴f′(x)≤0,
∴函数f(x)在[1,+∞)上单调减
∴函数f(x)的单调减区间是[1,+∞).
(2)解:不等式
 ,即为
,即为 ,记
,记 ,
,所以
 ,
,令h(x)=x-lnx,则
 ,
,∵x≥1,∴h′(x)≥0.
∴h(x)在[1,+∞)上单调递增,∴[h(x)]min=h(1)=1>0,
从而g′(x)>0
故g(x)在[1,+∞)上也单调递增,
∴[g(x)]min=g(1)=2,所以k≤2
(3)证明:由(2)知:
 恒成立,即
恒成立,即 ,
,令x=n(n+1),则
 ,
,所以
 ,
, ,
, ,…,
,…, .
.叠加得:ln[1×22×32×…×n2×(n+1)]=

则1×22×32×…×n2×(n+1)>en-2,
所以[(n+1)!]2>(n+1)•en-2,(n∈N*).
分析:(1)求导函数,根据函数的定义域,即可确定函数的单调性;
(2)如果当x≥1时,不等式
 恒成立,把k分离出来,再利用导数法确定函数的单调性,再求出函数最值即可;
恒成立,把k分离出来,再利用导数法确定函数的单调性,再求出函数最值即可;(3)由(2)可得
 ,令x=n(n+1),则
,令x=n(n+1),则 ,写出n个式子,叠加即可证明结论.
,写出n个式子,叠加即可证明结论.点评:本题考查应用导数研究函数的极值最值问题,考查不等式的证明,有关恒成立的问题一般采取分离参数,转化为求函数的最值问题,体现了转化的思想方法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
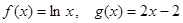 .
.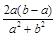 (闭区间[m,n]的长度定义为n –m).
(闭区间[m,n]的长度定义为n –m).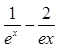 是否存在实数根?说明理由。
是否存在实数根?说明理由。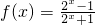
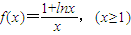
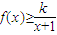 恒成立,求实数k的取值范围;
恒成立,求实数k的取值范围;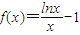
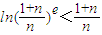 .
.