题目内容
 已知函数
已知函数 的最小正周期为π,且当x=
的最小正周期为π,且当x= 时,函数有最小值.
时,函数有最小值.
(1)求f(x)的解析式;
(2)作出f(x)在[0,π]范围内的大致图象.
解:(1)∵ =
= +1-
+1-
=1-sin .
.
由于它的最小正周期为π,故 =π,∴ω=1.
=π,∴ω=1.
故f(x)═1-sin .
.
(2)∵x∈[0,π],∴2x+ ∈[
∈[ ,
, ].列表如下:
].列表如下:
如图:
分析:(1)利用三角函数的恒等变换化简函数f(x)=1-sin ,再由它的周期等于π求出ω=1,故f(x)=1-sin
,再由它的周期等于π求出ω=1,故f(x)=1-sin .
.
(2)由x∈[0,π],可得 2x+ ∈[
∈[ ,
, ],列表作图即得所求.
],列表作图即得所求.
点评:本题主要考查三角函数的恒等变换,函数y=Asin(ωx+∅)的图象和性质,属于中档题.
 =
= +1-
+1-
=1-sin
 .
.由于它的最小正周期为π,故
 =π,∴ω=1.
=π,∴ω=1.故f(x)═1-sin
 .
.(2)∵x∈[0,π],∴2x+
 ∈[
∈[ ,
, ].列表如下:
].列表如下: 2x+ |  |  | π |  | 2π |  |
| x | 0 |  |  | 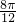 |  | π |
| sinx |  | 1 | 0 | -1 | 0 |  |
| f(x) |  | 0 | 1 | 2 | 1 |  |

分析:(1)利用三角函数的恒等变换化简函数f(x)=1-sin
 ,再由它的周期等于π求出ω=1,故f(x)=1-sin
,再由它的周期等于π求出ω=1,故f(x)=1-sin .
.(2)由x∈[0,π],可得 2x+
 ∈[
∈[ ,
, ],列表作图即得所求.
],列表作图即得所求.点评:本题主要考查三角函数的恒等变换,函数y=Asin(ωx+∅)的图象和性质,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的最小正周期为
的最小正周期为 ,将其图象向左平移
,将其图象向左平移 个单位长度,所得图象关于
个单位长度,所得图象关于 轴对称,则
轴对称,则 的一个可能值是
( )
的一个可能值是
( ) B.
B. C.
C. D.
D.
 的最小正周期为2π.
的最小正周期为2π. ,求
,求 的值.
的值. 的最小正周期为π,其图象关于直线
的最小正周期为π,其图象关于直线 对称.
对称. 上的单调递增区间;
上的单调递增区间; 上只有一个实数解,求实数m的取值范围.
上只有一个实数解,求实数m的取值范围. 的最小正周期为
的最小正周期为 .
.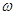 的值;
的值; 的最小正周期为
的最小正周期为
 的值;
的值;
 在
在
 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围.