题目内容

已知点G是圆F：(x+2)2+y2=4上任意一点，R（2，0），线段GR的垂直平分线交直线GF于H.

（1）求点H的轨迹C的方程；

（2）点M（1，0），P、Q是轨迹C上的两点，直线PQ过圆心F（-2，0），且F在线段PQ之间，求△PQM面积的最小值.

解：（1）点H的轨迹C的方程为x2=1.

（2）设P(x1,y1),Q(x2,y2),若PQ⊥x轴,则直线PQ:x=-2代入C的方程得y1=3,y2=-3,

S△PQM=S△PFM+S△QFM=×6×3=9.

若PQ不垂直于x轴，设直线PQ:y=k(x+2).

∵F在P、Q两点之间，∴P、Q在双曲线的左支上，且y1y2＜0.

又双曲线的渐近线为y=±x,∴k＜-或k＞,即|k|＞,联立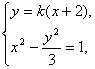

消去x，整理得(3-k2)y2-12ky+9k2=0.y1y2=,y1+y2=,

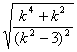∴|y1-y2|==6=6≥6

∴S△PQM=|y1-y2|×|FM|=|y1-y2|≥9.

综上可知：△PQM面积的最小值是9.

练习册系列答案
相关题目
已知椭圆E：
x2
a2
+
y2
b2
=1(a＞b＞0)的左、右焦点分别为F1，F2，点P是x轴上方椭圆E上的一点，且PF1⊥F1F2，|PF1|=
3
2
，|PF2|=
5
2
．
（Ⅰ） 求椭圆E的方程和P点的坐标；
（Ⅱ）判断以PF2为直径的圆与以椭圆E的长轴为直径的圆的位置关系；
（Ⅲ）若点G是椭圆C：
x2
m2
+
y2
n2
=1(m＞n＞0)上的任意一点，F是椭圆C的一个焦点，探究以GF为直径的圆与以椭圆C的长轴为直径的圆的位置关系．
已知双曲线E：
x2
24
-
y2
12
=1的左焦点为F，左准线l与x轴的交点是圆C的圆心，圆C恰好经过坐标原点O，设G是圆C上任意一点．
（Ⅰ）求圆C的方程；
（Ⅱ）若直线FG与直线l交于点T，且G为线段FT的中点，求直线FG被圆C所截得的弦长；
（Ⅲ）在平面上是否存在定点P，使得对圆C上任意的点G有
|GF|
|GP|
=
1
2
？若存在，求出点P的坐标；若不存在，请说明理由．
（2011•重庆一模）已知椭圆E：
x2
8
+
y2
4
=1的左焦点为F，左准线l与x轴的交点是圆C的圆心，圆C恰好经过坐标原点O，设G是圆C上任意一点．
（Ⅰ）求圆C的方程；
（Ⅱ）若直线FG与直线l交于点T，且G为线段FT的中点，求直线FG被圆C所截得的弦长；
（Ⅲ）在平面上是否存在一点P，使得
GF
GP
=
1
2
？若存在，求出点P坐标；若不存在，请说明理由．
（2012•青岛一模）已知点M在椭圆D：
x2
a2
+
y2
b2
=1（a＞b＞0）上，以M为圆心的圆与x轴相切于椭圆的右焦点，若圆M与y轴相交于A，B两点，且△ABM是边长为
2
6
3
的正三角形．
（Ⅰ）求椭圆D的方程；
（Ⅱ）设P是椭圆D上的一点，过点P的直线l交x轴于点F（-1，0），交y轴于点Q，若
QP
=2
PF
，求直线l的斜率；
（Ⅲ）过点G（0，-2）作直线GK与椭圆N：
3x2
a2
+
4y2
b2
=1左半部分交于H，K两点，又过椭圆N的右焦点F1做平行于HK的直线交椭圆N于R，S两点，试判断满足|GH|•|GK|=3|RF1|•|F1S|的直线GK是否存在？请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网