题目内容
若函数f(x)=-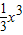 +x在(a,10-a2)上有最大值,则实数a的取值范围为 .
+x在(a,10-a2)上有最大值,则实数a的取值范围为 .
【答案】分析:根据题意求出函数的导数,因为函数f(x)=-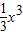 +x在(a,10-a2)上有最大值所以f′(x)先大于0然后再小于0,所以结合二次函数的性质可得:a<1<10-a2,
+x在(a,10-a2)上有最大值所以f′(x)先大于0然后再小于0,所以结合二次函数的性质可得:a<1<10-a2,
进而求出正确的答案.
解答:解:f′(x)=-x2+1.因为函数f(x)=-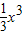 +x在(a,10-a2)上有最大值,
+x在(a,10-a2)上有最大值,
所以函数f(x)在(a,10-a2)内先增再减,f′(x)先大于0然后再小于0,所以结合二次函数的性质可得:a<1<10-a2,
解得-3<a<1
故答案为:(-3,1).
点评:解决此类问题的关键是熟练掌握导数的作用,即求函数的单调区间与函数的最值,并且进行正确的运算
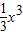 +x在(a,10-a2)上有最大值所以f′(x)先大于0然后再小于0,所以结合二次函数的性质可得:a<1<10-a2,
+x在(a,10-a2)上有最大值所以f′(x)先大于0然后再小于0,所以结合二次函数的性质可得:a<1<10-a2,进而求出正确的答案.
解答:解:f′(x)=-x2+1.因为函数f(x)=-
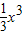 +x在(a,10-a2)上有最大值,
+x在(a,10-a2)上有最大值,所以函数f(x)在(a,10-a2)内先增再减,f′(x)先大于0然后再小于0,所以结合二次函数的性质可得:a<1<10-a2,
解得-3<a<1
故答案为:(-3,1).
点评:解决此类问题的关键是熟练掌握导数的作用,即求函数的单调区间与函数的最值,并且进行正确的运算

练习册系列答案
相关题目