题目内容
若函数f（x）=x+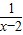
（x＞2）在x=a处取最小值，则a= ．
【答案】分析：将f（x）=x+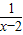
化成x-2+
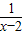+2，使x-2＞0，然后利用基本不等式可求出最小值，注意等号成立的条件，可求出a的值．
解答：解：f（x）=x+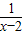
=x-2+
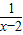+2≥4
当x-2=1时，即x=3时等号成立．
∵x=a处取最小值，
∴a=3
故答案为：3
点评：本题主要考查了基本不等式在最值问题中的应用，注意“一正、二定、三相等”，属于基础题．
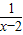化成x-2+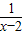+2，使x-2＞0，然后利用基本不等式可求出最小值，注意等号成立的条件，可求出a的值．解答：解：f（x）=x+
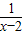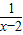=x-2++2≥4当x-2=1时，即x=3时等号成立．
∵x=a处取最小值，
∴a=3
故答案为：3
点评：本题主要考查了基本不等式在最值问题中的应用，注意“一正、二定、三相等”，属于基础题．
练习册系列答案
考前必练系列答案
相关题目
若函数f（x）（x∈R）为奇函数，且存在反函数f-1（x）（与f（x）不同），F(x)=
，则下列关于函数F（x）的奇偶性的说法中正确的是（ ）
| 2f(x)-2f-1(x) |
| 2f(x)+2f-1(x) |
| A、F（x）是奇函数非偶函数 |
| B、F（x）是偶函数非奇函数 |
| C、F（x）既是奇函数又是偶函数 |
| D、F（x）既非奇函数又非偶函数 |