题目内容
在空间中,给出下列4个命题(其中a、b、c表示直线,β表示平面),则正确命题的序号是( )(1)三个点确定一个平面;
(2)若a∥c,b∥c,则a∥b;
(3)在空间中,若角θ1与角θ2的两边分别平行,则θ1=θ2;
(4)若a⊥b,a⊥c,b、c?β,则α⊥β.
A.(1)、(2)、(4)
B.(2)
C.(2)、(3)
D.(2)、(3)、(4)
【答案】分析:根据公理2,我们可以判断(1)的真假;根据平行公理,我们可以判断(2)的真假;根据平行解定理,我们可以判断(3)的真假;根据线面垂直的性质及判定方法,可以判断(4)的真假,进而得到答案.
解答:解:(1)中,若三点共线,则不能确定一平面,故(1)错误;
(2)中,若a||c,b||c,由平行公理,可得a||b,故(2)正确;
(3)中,在空间中,若角θ1与角θ2的两边分别平行,则θ1与θ2相等或互补,故(3)错误;
(4)中,若b,c相交,则a⊥β,若b,c平行,则a⊥β不一定成立,故(4)错误;
故选B
点评:本题考查的知识点是空间中直线与平面之间的位置关系,平面的基本性质,熟练掌握立体几何中的相关基础知识点是解答本题的关键.
解答:解:(1)中,若三点共线,则不能确定一平面,故(1)错误;
(2)中,若a||c,b||c,由平行公理,可得a||b,故(2)正确;
(3)中,在空间中,若角θ1与角θ2的两边分别平行,则θ1与θ2相等或互补,故(3)错误;
(4)中,若b,c相交,则a⊥β,若b,c平行,则a⊥β不一定成立,故(4)错误;
故选B
点评:本题考查的知识点是空间中直线与平面之间的位置关系,平面的基本性质,熟练掌握立体几何中的相关基础知识点是解答本题的关键.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
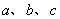 表示直线,
表示直线,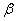 表示平面),则正确命题的序号是
[答]( )
表示平面),则正确命题的序号是
[答]( )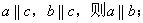
 的两边分别平行,则
的两边分别平行,则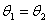 ;
; .
.