题目内容
设函数 的定义域为集合A,函数
的定义域为集合A,函数 的定义域为集合B.
的定义域为集合B.
(1)求证:函数f(x)的图象关于原点成中心对称.
(2)a≥2是A∩B= 的什么条件(充分非必要条件、必要非充分条件、充要条件、既非充分也非必要条件)?并证明你的结论.
的什么条件(充分非必要条件、必要非充分条件、充要条件、既非充分也非必要条件)?并证明你的结论.
 的定义域为集合A,函数
的定义域为集合A,函数 的定义域为集合B.
的定义域为集合B.(1)求证:函数f(x)的图象关于原点成中心对称.
(2)a≥2是A∩B=
 的什么条件(充分非必要条件、必要非充分条件、充要条件、既非充分也非必要条件)?并证明你的结论.
的什么条件(充分非必要条件、必要非充分条件、充要条件、既非充分也非必要条件)?并证明你的结论.证明:(1)∵ ﹣1>0,
﹣1>0,
∴ <0,
<0,
∴﹣1<x<1
∴A=(﹣1,1),
故f(x)的定义域关于原点对称
又f(x)=lg ,则 f(﹣x)=lg
,则 f(﹣x)=lg =lg
=lg =﹣lg
=﹣lg ,
,
∴f(x)是奇函数.即函数f(x)的图象关于原点成中心对称
(2)∵B={x|x2+2ax﹣1+a2≤0}
,∴﹣1﹣a≤x≤1﹣a,即B=[﹣1﹣a,1﹣a]
当a≥2时,﹣1﹣a≤﹣3,1﹣a≤﹣1,由A=(﹣1,1),B=[﹣1﹣a,1﹣a],有A∩B=
反之,若A∩B= ,可取﹣a﹣1=2,则a=﹣3,a小于2,
,可取﹣a﹣1=2,则a=﹣3,a小于2,
所以a≥2是A∩B= 的充分非必要条件
的充分非必要条件
 ﹣1>0,
﹣1>0,∴
 <0,
<0, ∴﹣1<x<1
∴A=(﹣1,1),
故f(x)的定义域关于原点对称
又f(x)=lg
 ,则 f(﹣x)=lg
,则 f(﹣x)=lg =lg
=lg =﹣lg
=﹣lg ,
,∴f(x)是奇函数.即函数f(x)的图象关于原点成中心对称
(2)∵B={x|x2+2ax﹣1+a2≤0}
,∴﹣1﹣a≤x≤1﹣a,即B=[﹣1﹣a,1﹣a]
当a≥2时,﹣1﹣a≤﹣3,1﹣a≤﹣1,由A=(﹣1,1),B=[﹣1﹣a,1﹣a],有A∩B=

反之,若A∩B=
 ,可取﹣a﹣1=2,则a=﹣3,a小于2,
,可取﹣a﹣1=2,则a=﹣3,a小于2,所以a≥2是A∩B=
 的充分非必要条件
的充分非必要条件
练习册系列答案
相关题目
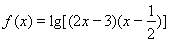

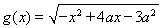
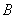
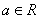

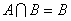
 .
. 的定义域为集合B,若A⊆B,求实数a的取值范围.
的定义域为集合B,若A⊆B,求实数a的取值范围. 的定义域为集合A,函数
的定义域为集合A,函数 的定义域为集合B。
的定义域为集合B。 ,求实数
,求实数 的取值范围。
的取值范围。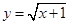 的定义域为集合
的定义域为集合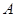 ,不等式
,不等式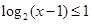 的解集为集合
的解集为集合 .
.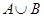 ,
,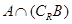 .
.