题目内容
曲线 与
与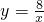 在它们交点处的两条切线与轴所围成的三角形的面积为________.
在它们交点处的两条切线与轴所围成的三角形的面积为________.
12
分析:先联立方程,求出两曲线交点,再分别对 与
与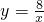 求导,利用导数,求出两曲线在交点处的切线斜率,利用点斜式求出切线方程,找到两切线与x轴交点,最后用面积公式计算面积即可.
求导,利用导数,求出两曲线在交点处的切线斜率,利用点斜式求出切线方程,找到两切线与x轴交点,最后用面积公式计算面积即可.
解答:曲线 与
与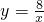 ,它们的交点坐标是(4,2),
,它们的交点坐标是(4,2),
两条切线方程分别是y= x+1和y=-
x+1和y=- x+4,
x+4,
y=0时,x=-4,x=8,
于是三角形三顶点坐标分别为 (4,2);(-4,0);(8,0),
它们与x轴所围成的三角形的面积是 .
.
故答案为:12.
点评:本题考查了利用导数求切线斜率,属于导数的应用.应当掌握.
分析:先联立方程,求出两曲线交点,再分别对
 与
与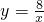 求导,利用导数,求出两曲线在交点处的切线斜率,利用点斜式求出切线方程,找到两切线与x轴交点,最后用面积公式计算面积即可.
求导,利用导数,求出两曲线在交点处的切线斜率,利用点斜式求出切线方程,找到两切线与x轴交点,最后用面积公式计算面积即可.解答:曲线
 与
与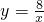 ,它们的交点坐标是(4,2),
,它们的交点坐标是(4,2),两条切线方程分别是y=
 x+1和y=-
x+1和y=- x+4,
x+4,y=0时,x=-4,x=8,
于是三角形三顶点坐标分别为 (4,2);(-4,0);(8,0),
它们与x轴所围成的三角形的面积是
 .
.故答案为:12.
点评:本题考查了利用导数求切线斜率,属于导数的应用.应当掌握.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
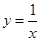 和
和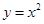 在它们交点处的两条切线与
在它们交点处的两条切线与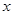 轴所围成的三角形面积是
轴所围成的三角形面积是 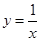 和
和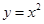 在它们交点处的两条切线与
在它们交点处的两条切线与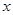 轴所围成的三角形面积是
轴所围成的三角形面积是  和
和 在它们交点处的两条切线与
在它们交点处的两条切线与 轴所围成的三角形面积是
。
轴所围成的三角形面积是
。 与
与 在它们交点处的两条切线与x轴所围成的三角形的面积为 .
在它们交点处的两条切线与x轴所围成的三角形的面积为 .