题目内容
已知函数 .
.
(1)若 在
在 上是增函数,求
上是增函数,求 的取值范围;
的取值范围;
(2)若 在
在 处取得极值,且
处取得极值,且 时,
时, 恒成立,求
恒成立,求 的取值范围.
的取值范围.
 .
.(1)若
 在
在 上是增函数,求
上是增函数,求 的取值范围;
的取值范围;(2)若
 在
在 处取得极值,且
处取得极值,且 时,
时, 恒成立,求
恒成立,求 的取值范围.
的取值范围.解:(1) ,因为
,因为 在
在 上是增函数,所以
上是增函数,所以 对
对 恒成立,
恒成立,
即 对
对 恒成立,只需
恒成立,只需 ,所以
,所以 。
。
当 时,
时, 对
对 恒成立,满足
恒成立,满足 在
在 上是增函数。
上是增函数。
(2)因为 在
在 处取得极值,所以
处取得极值,所以 ,
, ,此时
,此时
 ,
, ,
,
令 ,得
,得 或
或 。
。
当 变化时,
变化时, 、
、 的变化情况如下:
的变化情况如下:
 ,比较知道,
,比较知道, 时,
时, 的最大值为
的最大值为 ,只需
,只需 ,解得
,解得 或
或 。
。
 ,因为
,因为 在
在 上是增函数,所以
上是增函数,所以 对
对 恒成立,
恒成立,即
 对
对 恒成立,只需
恒成立,只需 ,所以
,所以 。
。当
 时,
时, 对
对 恒成立,满足
恒成立,满足 在
在 上是增函数。
上是增函数。(2)因为
 在
在 处取得极值,所以
处取得极值,所以 ,
, ,此时
,此时 ,
, ,
,令
 ,得
,得 或
或 。
。当
 变化时,
变化时, 、
、 的变化情况如下:
的变化情况如下: | -1 |  |  |  | 1 |  | 2 |
 | | + | 0 | — | 0 | + | + |
 |  |  | 极大值 |  | 极小值 |  | |
 ,比较知道,
,比较知道, 时,
时, 的最大值为
的最大值为 ,只需
,只需 ,解得
,解得 或
或 。
。本题主要考查函数的导数以及导数的应用(函数单调性与极值最值问题),不等式的恒成立问题的处理。

练习册系列答案
相关题目
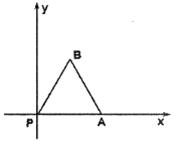
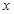 轴滚动,设顶点
轴滚动,设顶点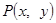 的纵坐标与横坐标的函数关系式是
的纵坐标与横坐标的函数关系式是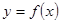 ,
,
 在区间
在区间
 内有零点,则( )
内有零点,则( )


 的符号不定
的符号不定 根的个数为( )
根的个数为( )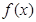 是定义在
是定义在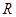 上且以3为周期的奇函数,当
上且以3为周期的奇函数,当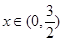 时,
时,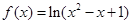 ,则函数
,则函数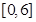 上的零点个数是
上的零点个数是  ,且函数
,且函数 恰有3个不同的零点,则实数a的取值范围是 ( )
恰有3个不同的零点,则实数a的取值范围是 ( )


 是
是 的零点,若
的零点,若 ,则
,则 的值满足( )
的值满足( )


 有 个零点.
有 个零点. 为实数,且
为实数,且
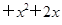 =-2,则
=-2,则 的值为________________。
的值为________________。