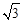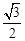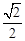题目内容
过双曲线的一个焦点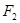 作垂直于实轴的弦
作垂直于实轴的弦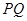 ,
,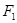 是另一焦点,若∠
是另一焦点,若∠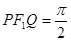 ,则双曲线的离心率
,则双曲线的离心率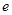 等于( )
等于( )
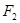 作垂直于实轴的弦
作垂直于实轴的弦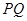 ,
,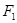 是另一焦点,若∠
是另一焦点,若∠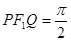 ,则双曲线的离心率
,则双曲线的离心率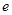 等于( )
等于( )A.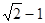 | B. | C. | D.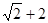 |
C
试题分析:解:由题意可知|PF2| =
 ,|F1F2|=2c,∵∠PF1Q=
,|F1F2|=2c,∵∠PF1Q= ,∴2(4c2+
,∴2(4c2+ )=
)= ,∴4a2c2=b4=(c2-a2)2=c4-2a2c2+a4,整理得e4-6e2+1=0,解得e=
,∴4a2c2=b4=(c2-a2)2=c4-2a2c2+a4,整理得e4-6e2+1=0,解得e= +1或e=
+1或e= -1(舍去)故选C.
-1(舍去)故选C.点评:本题考查双曲线的离心率,解题要注意时双曲线的离心率大于1.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
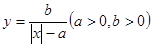 的函数称为“莫言函数”,并把其与
的函数称为“莫言函数”,并把其与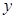 轴的交点关于原点的对称点称为“莫言点”,以“莫言点”为圆心凡是与“莫言函数”图象有公共点的圆,皆称之为“莫言圆”.当
轴的交点关于原点的对称点称为“莫言点”,以“莫言点”为圆心凡是与“莫言函数”图象有公共点的圆,皆称之为“莫言圆”.当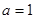 ,
,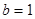 时,在所有的“莫言圆”中,面积的最小值 .
时,在所有的“莫言圆”中,面积的最小值 .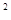 =4x,O为坐标原点,P为抛物线的准线与其对称轴的交点,过焦点F且垂直于x轴的直线交抛物线于M、N两点,若直线PM与ON相交于点Q,则cos∠MQN=
=4x,O为坐标原点,P为抛物线的准线与其对称轴的交点,过焦点F且垂直于x轴的直线交抛物线于M、N两点,若直线PM与ON相交于点Q,则cos∠MQN=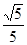
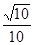
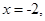 则抛物线的方程是( )
则抛物线的方程是( ) 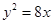
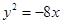
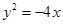
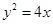
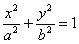
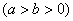 的离心率是
的离心率是 ,则双曲线
,则双曲线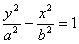 的渐近线方程是( )
的渐近线方程是( )
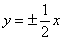


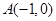 和
和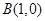 ,动点
,动点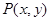 在直线
在直线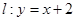 上移动,椭圆
上移动,椭圆 以
以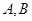 为焦点且经过点
为焦点且经过点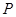 ,记椭圆
,记椭圆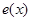 ,则函数
,则函数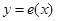 的大致图像是( )
的大致图像是( )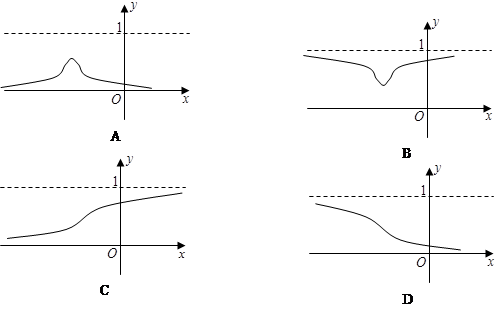
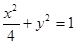 的焦点为
的焦点为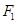 ,
,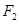 ,在长轴
,在长轴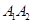 上任取一点
上任取一点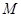 ,过
,过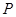 ,则使得
,则使得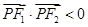 的点
的点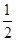
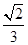

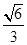
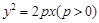 的焦点为
的焦点为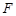 ,点
,点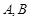 在此抛物线上,且
在此抛物线上,且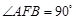 ,弦
,弦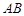 的中点
的中点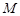 在该抛物线准线上的射影为
在该抛物线准线上的射影为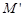 ,则
,则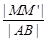 的最大值为( )
的最大值为( )