Question

已知函数f(x)＝x³－3ax²－bx，其中a，b为实数．

(1)若f(x)在x＝1处取得的极值为2，求a，b的值；

(2)若f(x)在区间[－1,2]上为减函数，且b＝9a，求a的取值范围．

Answer 1

(1)由题设可知：f′(1)＝0且f(1)＝2，

即解得

(2)∵当a≠0时，f′(x)＝3x²－6ax－b＝3x²－6ax－9a，又f(x)在[－1,2]上为减函数，

∴f′(x)≤0对x∈[－1,2]恒成立，

即3x²－6ax－9a≤0对x∈[－1,2]恒成立，

∴f′(－1)≤0且f′(2)≤0，

即⇒⇒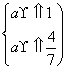a≥1.