题目内容
已知函数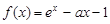 (e为自然对数的底数),a>0.
(e为自然对数的底数),a>0.
(1)若函数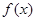 恰有一个零点,证明:
恰有一个零点,证明: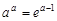 ;
;
(2)若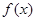 ≥0对任意x∈R恒成立,求实数a的取值集合.
≥0对任意x∈R恒成立,求实数a的取值集合.
(1)见解析;(2){1}.
解析试题分析:(1)先判断f(x)的单调性,根据“f(x)前有一个零点”,找到关于a的等式,化简整理可得需证结论;(2)根据(1),只需f(x)的最小值不小于0即可.
试题解析:(1)证明: 由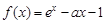 ,得
,得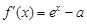 . 1分
. 1分
由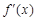 >0,即
>0,即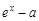 >0,解得x>lna,同理由
>0,解得x>lna,同理由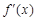 <0解得x<lna,
<0解得x<lna,
∴ f(x)在(-∞,lna)上是减函数,在(lna,+∞)上是增函数,
于是f(x)在x=lna取得最小值.
又∵ 函数f(x)恰有一个零点,则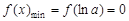 , 4分
, 4分
即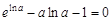 . 5分
. 5分
化简得: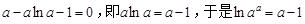 ,
,
∴ 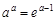 . 6分
. 6分
(2)解:由(1)知,f(x)在x=lna取得最小值f(lna),
由题意得f(lna)≥0,即a-alna-1≥0, 8分
令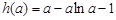 ,则
,则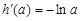 ,
,
由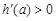 可得0<a<1,由
可得0<a<1,由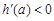 可得a>1.
可得a>1.
∴ h(a)在(0,1)上单调递增,在(1,+∞)上单调递减,即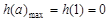 ,
,
∴ 当0<a<1或a>1时,h(a)<0,
∴ 要使得f(x)≥0对任意x∈R恒成立,a=1
∴ a的取值集合为{1} 13分
考点:导数,函数的零点,恒成立问题

练习册系列答案
相关题目
设函数f(x)= ,若f(α)=4,则实数α=( )
,若f(α)=4,则实数α=( )
| A.-4或-2 | B.-4或2 |
| C.-2或4 | D.-2或2 |
函数 在(1,1)处的切线方程为( )
在(1,1)处的切线方程为( )
A. | B. |
C. | D. |
函数 存在与直线
存在与直线 平行的切线,则实数
平行的切线,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C.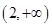 | D.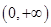 |
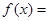
 ,则
,则 = .
= . 的
的 的取值集合是 .
的取值集合是 .

 的图像可能是( ) .
的图像可能是( ) .



 的终边过点P(-12,5),则
的终边过点P(-12,5),则 .
.