题目内容
一同学在电脑中打出如下若干个圆:○●○○●○○○●○○○○●○○○○○●…,若依此规律继续下去,得到一系列的圆,则在前2012个圆中共有●的个数是( )A.61
B.62
C.63
D.64
【答案】分析:将圆分组:把每个实心圆和它前面的连续的空心圆看成一组,那么每组圆的总个数就等于2,3,4,…,构成等差数列.根据等差数列的求和公式可以算出第2012个圆在之前有多少个整组,即可得答案.
解答:解:解:根据题意,将圆分组:
第一组:○●,有2个圆;
第二组:○○●,有3个圆;
第三组:○○○●,有4个圆;
…
每组的最后为一个实心圆;
每组圆的总个数构成了一个等差数列,前n组圆的总个数为
sn=2+3+4+…+(n+1)=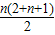 =
=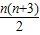
因为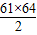 =1952<2011<
=1952<2011<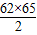 =2015
=2015
则在前2012个圈中包含了61个整组,和第62组的一部分,
即有61个黑圆,
故选A
点评:本题考查归纳推理的应用,解题的关键是找出图形的变化规律,构造等差数列,然后利用等差数列的求和公式计算,属基础题.
解答:解:解:根据题意,将圆分组:
第一组:○●,有2个圆;
第二组:○○●,有3个圆;
第三组:○○○●,有4个圆;
…
每组的最后为一个实心圆;
每组圆的总个数构成了一个等差数列,前n组圆的总个数为
sn=2+3+4+…+(n+1)=
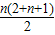 =
=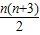
因为
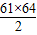 =1952<2011<
=1952<2011<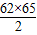 =2015
=2015则在前2012个圈中包含了61个整组,和第62组的一部分,
即有61个黑圆,
故选A
点评:本题考查归纳推理的应用,解题的关键是找出图形的变化规律,构造等差数列,然后利用等差数列的求和公式计算,属基础题.

练习册系列答案
相关题目