题目内容
已知直三棱柱ABC—A1B1C1中,AB=4,AC=AA1=2,∠CAB=60°.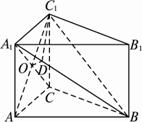
(1)求证:A1C⊥B1C1;
(2)求点B1到平面A1BC的距离;
(3)求二面角C1-A1B-C的大小.
解法一:(1)在△ABC中,BC2=AB2+AC2-2AB·AC·cos∠BAC=16+4-16cos60°=12,?
 ?
?
∴BC=![]() ,AC2+BC2=AB2.??
,AC2+BC2=AB2.??
∴∠ACB=90°,即BC⊥AC.?
由直三棱柱性质知:平面ACC1A1⊥平面ABC.
∴BC⊥平面ACC1A1.
∴BC⊥A1C.?
又BC∥B1C1,∴B1C1⊥A1C.?
(2)∵BC∥B1C1,BC![]() 平面ABC,
平面ABC,
∴B1C1∥平面A1CB.?
∴B1点到平面A1CB的距离等于点C1到平面A1CB的距离.?
设点B1到平面A1CB的距离为h,则?
VB1—A1BC?=VC1—A1BC?=VB—A1C1C?.?
∴h=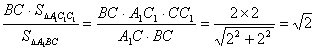 .?
.?
(3)连结AC1,交A1C于O,过O作OD⊥A1B于D,连结C1D.?
由(1)BC⊥平面ACC1A1,得平面BCA1⊥平面ACC1A1.?
由正方形ACC1A1知AC1⊥A1C,
∴C1A⊥平面A1BC.?
∴OD是C1D在平面A1BC上的射影?.?
∴C1D⊥A1B(三垂线定理).?
∴∠ODC1是二面角C1-A1B-C的平面角.?
在△A1BC中,A1B=![]() ,BC=
,BC=![]() ,A1C=
,A1C=![]() ,A1O=
,A1O=![]() .??
.??
由![]() ,得OD=
,得OD=![]() ,?
,?
∴tan∠ODC1=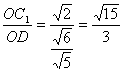 .?
.?
∴二面角C1-A1B-C的大小是arctan![]() .?
.?
解法二:先证∠ACB=90°,然后以C为原点,分别以CA、CB、CC1为x轴、y轴、z轴建立空间直角坐标系.(略).

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
 如图,已知直三棱柱ABC-A1B1C1,∠ACB=90°,AC=BC=2,AA1=4.E、F分别是棱CC1、AB中点.
如图,已知直三棱柱ABC-A1B1C1,∠ACB=90°,AC=BC=2,AA1=4.E、F分别是棱CC1、AB中点.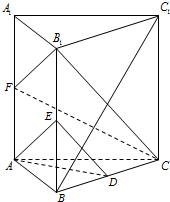 已知直三棱柱ABC-A1B1C1的所有棱长都相等,且D,E,F分别为BC,BB1,AA1的中点.
已知直三棱柱ABC-A1B1C1的所有棱长都相等,且D,E,F分别为BC,BB1,AA1的中点. 如图所示,已知直三棱柱ABC-A′B′C′,AC=AB=AA′=2,AC,AB,AA′两两垂直,E,F,H分别是AC,AB,BC的中点,
如图所示,已知直三棱柱ABC-A′B′C′,AC=AB=AA′=2,AC,AB,AA′两两垂直,E,F,H分别是AC,AB,BC的中点, 如图,已知直三棱柱ABC-A1B1C1的侧棱长为2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,D是A A1的中点.
如图,已知直三棱柱ABC-A1B1C1的侧棱长为2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,D是A A1的中点. 如图,已知直三棱柱ABC-A1B1C1中,AB=AC;M.N.P分别是棱BC.CC1.B1C1的中点.
如图,已知直三棱柱ABC-A1B1C1中,AB=AC;M.N.P分别是棱BC.CC1.B1C1的中点.