题目内容
已知lg(7•2x+8)≥log
2x,求函数f(x)=log
x•log
的最值及对应x的值.
| 10 |
| 1 |
| 2 |
| 1 |
| 2 |
| x |
| 4 |
∵lg(7•2x+8)≥log
2x,∴7•2x+8≥22x,解得x≤3.∴log
x≥log
3.
∴函数f(x)=log
x•log
=log
x(log
x+2)=(log
x)2+2log
x=(log
x+1)2-1
∴当log
x=-1时,函数f(x)=log
x•log
的最小值为-1,此时x=2.
| 10 |
| 1 |
| 2 |
| 1 |
| 2 |
∴函数f(x)=log
| 1 |
| 2 |
| 1 |
| 2 |
| x |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴当log
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| x |
| 4 |

练习册系列答案
相关题目
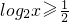 ,求函数
,求函数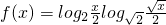 的最大值和最小值.
的最大值和最小值.