题目内容
已知平面向量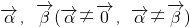 满足
满足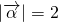 ,且
,且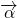 与
与  的夹角为120°,则
的夹角为120°,则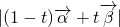 (t∈R)的最小值是________.
(t∈R)的最小值是________.

分析:由已知中中平面向量
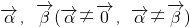 满足
满足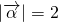 ,且
,且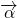 与
与  的夹角为120°,我们根据向量加法的三角形法则,可得当t|
的夹角为120°,我们根据向量加法的三角形法则,可得当t| |=
|= 时,
时,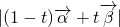 (t∈R)取最小值,进而求出
(t∈R)取最小值,进而求出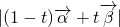 (t∈R)的最小值.
(t∈R)的最小值.解答:∵平面向量
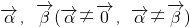 满足
满足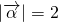 ,且
,且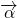 与
与  的夹角为120°,
的夹角为120°,故当t(
 )满足t|
)满足t| |=
|= 时,
时,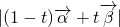 (t∈R)取最小值
(t∈R)取最小值此时由向量加法的三角形法则可得
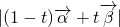 (t∈R)的最小值是
(t∈R)的最小值是
故答案为:

点评:本题考查的知识点是向量的模,向量在几何中的应用,其中根据
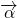 与
与  的夹角为120°,结合向量加法的三角形法则,及连接直线上的点与直线外一点的线段中,垂线段最短得到当t|
的夹角为120°,结合向量加法的三角形法则,及连接直线上的点与直线外一点的线段中,垂线段最短得到当t| |=
|= 时,
时,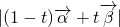 (t∈R)取最小值,是解答本题的关键.
(t∈R)取最小值,是解答本题的关键. 
练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
 满足
满足 ,且
,且 与
与 的夹角为120°,
的夹角为120°, ,则
,则 的取值范围是
.
的取值范围是
. 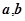 满足
满足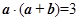 ,且
,且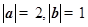 ,则向量
,则向量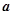 与
与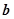 的夹角为
的夹角为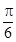 B.
B.
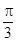 C.
C. 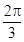 D.
D. 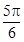
 满足
满足 ,且
,且 与
与 的夹角为120°,
的夹角为120°, ,则
,则 的取值范围是 ▲ .
的取值范围是 ▲ .