Question

某厂生产甲、乙两种产品，产量分别为45个、50个，所用原料为A、B两种规格的金属板，每张面积分别为2m²、3m²，用A种金属板可造甲产品3个，乙产品5个，用B种金属板可造甲、乙产品各6个，则A、B两种金属板各取多少张时，能完成计划并能使总用料面积最省？（　　）

A．A用2张，B用6张	B．A用4张，B用5张
C．A用3张，B用5张	D．A用3张，B用6张

Answer 1

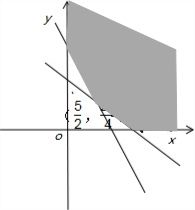
设A、B两种金属板各取x，y张
则满足的约束条件为：

3x+6y≥45 5x+6y≥50 x≥0 y≥0

总用料面积函数为：Z=2x+3y
在点(

5

2

，

25

4

)，目标函数取得最小值，
即当A、B两种金属板各取3，6张时，能完成计划并能使总用料面积最省．