题目内容
已知点F1,F2分别是椭圆为C: 的左、右焦点,过点F1(-c,0)作x轴的垂线交椭圆C的上半部分于点P,过点F2作直线PF2的垂线交直线
的左、右焦点,过点F1(-c,0)作x轴的垂线交椭圆C的上半部分于点P,过点F2作直线PF2的垂线交直线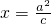 于点Q,若直线PQ与双曲线
于点Q,若直线PQ与双曲线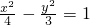 的一条渐近线平行,则椭圆的离心率为
的一条渐近线平行,则椭圆的离心率为
- A.

- B.

- C.

- D.

C
分析:将点P(-c,y1)(y1>0)代入C: ,得P(-c,
,得P(-c, ),由过点F2作直线PF2的垂线交直线
),由过点F2作直线PF2的垂线交直线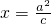 于点Q,PF2⊥QF2,得Q(
于点Q,PF2⊥QF2,得Q( ,2a),由直线PQ与双曲线
,2a),由直线PQ与双曲线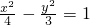 的一条渐近线平行,知
的一条渐近线平行,知 ,由此能求出结果.
,由此能求出结果.
解答:将点P(-c,y1)(y1>0)代入C: ,
,
得y1= ,
,
∴P(-c, ),
),
∵过点F2作直线PF2的垂线交直线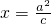 于点Q,PF2⊥QF2,
于点Q,PF2⊥QF2,
∴设Q( ,y),得
,y),得 ,解得y=2a,∴Q(
,解得y=2a,∴Q( ,2a),
,2a),
∵直线PQ与双曲线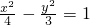 的一条渐近线平行,
的一条渐近线平行,
∴ ,即4a-
,即4a-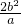 =
=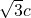 +
+ ,
,
整理,得2e3- +2e-
+2e- =0,
=0,
解得e= .
.
故选C.
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查导数知识的运用,综合性强.解题时要认真审题,注意等价转化思想的合理运用.
分析:将点P(-c,y1)(y1>0)代入C:
 ,得P(-c,
,得P(-c, ),由过点F2作直线PF2的垂线交直线
),由过点F2作直线PF2的垂线交直线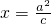 于点Q,PF2⊥QF2,得Q(
于点Q,PF2⊥QF2,得Q( ,2a),由直线PQ与双曲线
,2a),由直线PQ与双曲线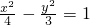 的一条渐近线平行,知
的一条渐近线平行,知 ,由此能求出结果.
,由此能求出结果.解答:将点P(-c,y1)(y1>0)代入C:
 ,
,得y1=
 ,
,∴P(-c,
 ),
),∵过点F2作直线PF2的垂线交直线
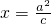 于点Q,PF2⊥QF2,
于点Q,PF2⊥QF2,∴设Q(
 ,y),得
,y),得 ,解得y=2a,∴Q(
,解得y=2a,∴Q( ,2a),
,2a),∵直线PQ与双曲线
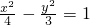 的一条渐近线平行,
的一条渐近线平行,∴
 ,即4a-
,即4a-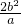 =
=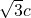 +
+ ,
,整理,得2e3-
 +2e-
+2e- =0,
=0,解得e=
 .
.故选C.
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查导数知识的运用,综合性强.解题时要认真审题,注意等价转化思想的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (a>b>0)的左、右焦点,点P为椭圆上任意一点,P到焦点F2的距离的最大值为
(a>b>0)的左、右焦点,点P为椭圆上任意一点,P到焦点F2的距离的最大值为 +1,且△PF1F2的最大面积为1。
+1,且△PF1F2的最大面积为1。 ,过点F2且斜率为k的直线L与椭圆C相交于A,B两点。对于任意的k∈R,
,过点F2且斜率为k的直线L与椭圆C相交于A,B两点。对于任意的k∈R, 是否为定值?若是求出这个定值;若不是说明理由。
是否为定值?若是求出这个定值;若不是说明理由。  的左右焦点,P是椭圆C上的一点,且
的左右焦点,P是椭圆C上的一点,且 的面积为
的面积为
 ,过点F2且斜率为k的直线l与椭圆C相交于A,B两点,对于任意的
,过点F2且斜率为k的直线l与椭圆C相交于A,B两点,对于任意的 是否为定值?若是求出这个定值;若不是说明理由.
是否为定值?若是求出这个定值;若不是说明理由.