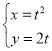题目内容
【题目】椭圆![]() 〔
〔![]() >b>0〕与抛物线
>b>0〕与抛物线![]() 有共同的焦点F,且两曲线在第一象限的交点为M,满足
有共同的焦点F,且两曲线在第一象限的交点为M,满足![]() .
.
(1)求椭圆的方程;
(2)过点![]() ,斜率为
,斜率为![]() 的直线
的直线![]() 与椭圆交于
与椭圆交于![]() 两点,设
两点,设![]() ,假设
,假设![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)由题可得,![]() ,点M的横坐标为
,点M的横坐标为![]() ,代入抛物线
,代入抛物线![]() 方程可求得M点纵坐标,然后利用椭圆的定义求出a,即可得到本题答案;
方程可求得M点纵坐标,然后利用椭圆的定义求出a,即可得到本题答案;
(2)联立直线方程与椭圆方程,利用韦达定理得![]() ①,
①,![]() ②,由题,得
②,由题,得![]() ③,结合以上三个式子,得
③,结合以上三个式子,得![]() ,求出
,求出![]() 在
在![]() 的取值范围,即可得到本题答案.
的取值范围,即可得到本题答案.
(1)由椭圆与抛物线![]() 有共同的焦点F,且两曲线在第一象限的交点为M,满足
有共同的焦点F,且两曲线在第一象限的交点为M,满足![]() ,
,
得椭圆的![]() ,点M的横坐标为
,点M的横坐标为![]() ,代入抛物线
,代入抛物线![]() 方程,可得
方程,可得 ,
,
因为椭圆焦点为![]() ,所以
,所以 ,得
,得![]() ,则椭圆的方程为
,则椭圆的方程为![]() ;
;
(2)设直线![]() 的方程为
的方程为![]() ,代入椭圆方程得:
,代入椭圆方程得:![]() ,
,![]() 恒成立.
恒成立.
设![]() ,那么
,那么![]() ①,
①,![]() ②,
②,
由![]() 可得,
可得,![]() ③,由以上三式可得:
③,由以上三式可得:![]() ,
,
当![]() 时,
时,![]() ,因此
,因此![]() 在
在![]() 上单调递增,
上单调递增,
因此当![]() 时,
时,![]() ,
,
因此,![]() ,解得
,解得![]() .
.

练习册系列答案
相关题目
【题目】生男生女都一样,女儿也是传后人.由于某些地区仍然存在封建传统思想,头胎的男女情况可能会影响生二孩的意愿,现随机抽取某地200户家庭进行调查统计.这200户家庭中,头胎为女孩的频率为0.5,生二孩的频率为0.525,其中头胎生女孩且生二孩的家庭数为60.
(1)完成下列![]() 列联表,并判断能否有95%的把握认为是否生二孩与头胎的男女情况有关;
列联表,并判断能否有95%的把握认为是否生二孩与头胎的男女情况有关;
生二孩 | 不生二孩 | 合计 | |
头胎为女孩 | 60 | ||
头胎为男孩 | |||
合计 | 200 |
(2)在抽取的200户家庭的样本中,按照分层抽样的方法在头胎生女孩家庭中抽取了5户,进一步了解情况,在抽取的5户中再随机抽取3户,求这3户中恰好有2户生二孩的概率.
附:
| 0.15 | 0.05 | 0.01 | 0.001 |
| 2.072 | 3.841 | 6.635 | 10.828 |
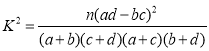 (其中
(其中![]() ).
).