题目内容
已知圆C：(x+1)2+y2=r2(r为常数，且r＞2)，定点B(1，0),A是圆C上的动点，直线AC与线段朋的垂直平分线l相交于点M．当点A在圆C上移动一周时，点M的轨迹记为曲线F．(1)求曲线F的方程；
(2)若点M在第一象限，且
=
,△CMB的面积S△CMB=
，求r的值及直线l的方程．
解：(1)连接MB，由题意有：
|MC|+|MB|=|MC|+|MA|=|AC|=r
又r＞|BC|=2
∴点M的轨迹是以C(-1，0)，B(1，0)为焦点的椭圆
∴a= c=l
∴曲线F的方程为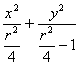：=1
(2)设M(x0，y0)，且x0、y0＞0
由于S△CMB=|CB|y0=y0=
所以M(x0，
)
又
=(x0+1，
)，
=(x0-1，
)
所以
·
=
所以x0=1，即M(1，
)
所以|MC|=
,|MB|=
所以r=|MC|+|MB|=4
(或用待定系数法将M(1，
)代入(1)中方程解出r)
点A分线段CM所成定比λ=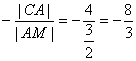
．
即点A坐标x=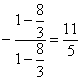
,y=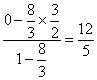
.
所以点A(
,
)
(或求出直线AC方程与圆C方程联立求出点A坐标)
所以KAB=
/(
-1)=2，又l⊥AB所以kl=
故直线l方程为：y-
(x-1)即x+2y-4=0
练习册系列答案
相关题目