题目内容
已知向量 =(
=( ),
), =(1,
=(1, )且
)且

 ,其中
,其中 ,则
,则 等于( )
等于( )
A. | B. | C. | D. |
D
解析试题分析:因为向量 =(
=( ),
), =(1,
=(1, )且
)且

 ,所以
,所以 ,所以
,所以 。因为
。因为 ,所以
,所以 >0,所以
>0,所以 .
.
考点:向量的数量积;向量垂直的条件;
点评:关于sinx,cosx的齐次式,往往化为关于tanx的式子。此题一定要注意判断三角函数值的符号。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设 R,向量
R,向量 ,且
,且 ,则
,则 ( )
( )
A.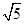 | B. | C. | D.10 |
已知两个非零向量 与
与 ,定义
,定义 ,其中
,其中 为
为 与
与 的夹角,若
的夹角,若 ,则
,则 的值为
的值为
A. | B. | C.6 | D.8 |
已知平面上不共线的四点O,A,B,C,若 则
则 的值为 ( )
的值为 ( )
A. | B. | C. | D. |
在空间直角坐标系中,若向量 ,则它们之间的关系是( )
,则它们之间的关系是( )
A. | B.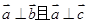 | C. | D. |
已知向量 ,
, ,若向量
,若向量 ,则
,则 ( )
( )
| A.2 | B. | C.8 | D. |
已知 D,E,F分别是△ABC的边AB,BC,CA的中点,则( )
A. | B. |
C.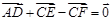 | D. |
已知 、
、 、
、 三点不共线,对平面
三点不共线,对平面 外的任一点
外的任一点 ,下列条件中能确定点
,下列条件中能确定点 与点
与点 、
、 、
、 一定共面的是( )
一定共面的是( )
A. | B. |
C. | D. |
已知向量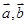 满足
满足 则向量
则向量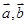 所成夹角为( )
所成夹角为( )
A.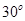 | B. | C.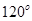 | D. |