题目内容
若关于x的函数f（x）=x2-2ax+2+a有两个零点，
（1）求a的取值范围．
（2）若两零点其中一个在（1，2）内，另一个在（2，3）内，求a的取值范围．
（1）求a的取值范围．
（2）若两零点其中一个在（1，2）内，另一个在（2，3）内，求a的取值范围．
（1）因为f（x）=x2-2ax+2+a有两个零点，
所以（-2a）2-4（2+a）＞0，即a＜-1或a＞2．
所以a的取值范围为：（-∞，-1）∪（2，+∞）．
（2）由两零点一个在（1，2）内，另一个在（2，3）内，
得
，即
，解得2＜a＜
．
所以a的取值范围为：（2，
）．
所以（-2a）2-4（2+a）＞0，即a＜-1或a＞2．
所以a的取值范围为：（-∞，-1）∪（2，+∞）．
（2）由两零点一个在（1，2）内，另一个在（2，3）内，
得
|
|
| 11 |
| 5 |
所以a的取值范围为：（2，
| 11 |
| 5 |
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
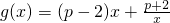，其中p≤0，若对任意的x∈[1，2]，总有2f（x）≥g（x）+4x-2x2成立，求p的取值范围．
，其中p≤0，若对任意的x∈[1，2]，总有2f（x）≥g（x）+4x-2x2成立，求p的取值范围．
，其中p≤0，若对任意的x∈[1，2]，总有2f（x）≥g（x）+4x-2x2成立，求p的取值范围．