题目内容
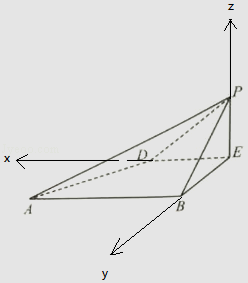
【题目】已知边长为2的菱形ABCD中,∠BCD=60°,E为DC的中点,如图1所示,将△BCE沿BE折起到△BPE的位置,且平面BPE⊥平面ABED,如图2所示. 
(Ⅰ)求证:△PAB为直角三角形;
(Ⅱ)求二面角A﹣PD﹣E的余弦值.
【答案】证明:(Ⅰ)∵边长为2的菱形ABCD中,∠BCD=60°,E为DC的中点,如图1所示, ∴BE⊥DC,AB∥CD,∴AB⊥BE,∴∠ABE=90°,
∵将△BCE沿BE折起到△BPE的位置,且平面BPE⊥平面ABED,如图2所示.
在翻折过程中,∠ABE=90°不变,
∴在△ABP中,∠ABP=90°,
∴△PAB为直角三角形.
解:(Ⅱ)由(Ⅰ)得∠BED=∠ABE=90°,∴DE⊥BE,
以E为原点,ED为x轴,EB为y轴,EP为z轴,建立空间直角坐标系,
A(2, ![]() ,0),P(0,0,1),D(1,0,0),E(0,0,0),
,0),P(0,0,1),D(1,0,0),E(0,0,0),![]() =(﹣1,0,1),
=(﹣1,0,1), ![]() =(1,
=(1, ![]() ,0),
,0), ![]() =(0,0,1),
=(0,0,1), ![]() =(1,0,0),
=(1,0,0),
设平面ADP的法向量 ![]() =(x,y,z),
=(x,y,z),
则 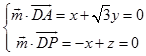 ,取x=
,取x= ![]() ,得
,得 ![]() =(
=( ![]() ),
),
平面PDE的法向量 ![]() =(1,0,0),
=(1,0,0),
设二面角A﹣PD﹣E的平面角为θ,
则cosθ= ![]() =
= ![]() =
= ![]() ,
,
∴二面角A﹣PD﹣E的余弦值为 ![]() .
.
【解析】(Ⅰ)推导出BE⊥DC,AB∥CD,从而AB⊥BE,进而∠ABE=90°,将△BCE沿BE折起到△BPE的位置,且平面BPE⊥平面ABED,在翻折过程中,∠ABE=90°不变,由此能证明△PAB为直角三角形.(Ⅱ)以E为原点,ED为x轴,EB为y轴,EP为z轴,建立空间直角坐标系,利用向量法能求出二面角A﹣PD﹣E的余弦值.
【考点精析】利用直线与平面垂直的性质对题目进行判断即可得到答案,需要熟知垂直于同一个平面的两条直线平行.

