题目内容
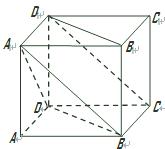
已知几何体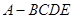 的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形.
的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形.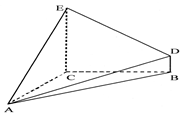
(Ⅰ)求此几何体的体积;
(Ⅱ)求异面直线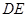 与
与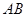 所成角的余弦值;
所成角的余弦值;
(Ⅲ)探究在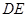 上是否存在点Q,使得
上是否存在点Q,使得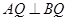 ,并说明理由.
,并说明理由.
(Ⅰ) (Ⅱ)
(Ⅱ) (Ⅲ) 在
(Ⅲ) 在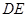 上存在点Q,使得
上存在点Q,使得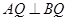 .
.
解析试题分析:(Ⅰ)由该几何体的三视图可知 垂直于底面
垂直于底面 ,且
,且 ,
, ,
,
 ,
, ,
,
此几何体的体积为 ;
;
解法一:(Ⅱ)过点 作
作 交
交 于
于 ,连接
,连接 ,则
,则 或其补角即为异面直线
或其补角即为异面直线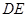
与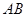 所成角,在
所成角,在 中,
中, ,
, ,
, ;即异面直线
;即异面直线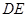 与
与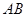 所成角的余弦值为
所成角的余弦值为 .
.
(Ⅲ)在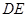 上存在点Q,使得
上存在点Q,使得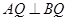 ;取
;取 中点
中点 ,过点
,过点 作
作 于点
于点 ,则点
,则点 为所求点;
为所求点;
连接 、
、 ,在
,在 和
和 中,
中,
 ,
,
 ∽
∽ ,
,
 ,
,
 ,
,
 ,
, ,
,
 ,
, ,
,
 ,
, 以
以 为圆心,
为圆心, 为直径的圆与
为直径的圆与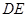 相切,切点为
相切,切点为 ,连接
,连接 、
、 ,可得
,可得 ;
;
 ,
, ,
,
 ,
,
 ,
, ,
,
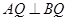 ;
;
解法二:(Ⅰ)同上。
(Ⅱ)以 为原点,以
为原点,以 、
、 、
、 所在直线为
所在直线为 、
、

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
 中,
中,
 底面
底面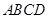 ,
,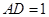 ,
,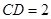 ,
,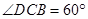 .
.
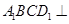 平面
平面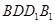 ;
;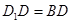 ,求四棱锥
,求四棱锥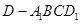 的体积.
的体积. 是边长为2的正方形,
是边长为2的正方形, ⊥平面
⊥平面 ,
, //
// 且
且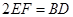 .
.
 ⊥平面
⊥平面 ;
; 的体积.
的体积. 
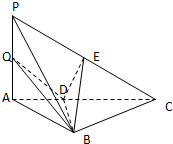
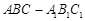 中,
中,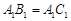 ,
,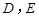 分 别是棱
分 别是棱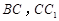 上的点(点
上的点(点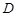 不同于点
不同于点 ),且
),且 为
为 的中点.
的中点.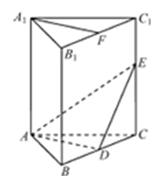
 平面
平面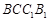 (2)直线
(2)直线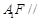 平面
平面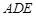
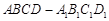 中.
中.
 与
与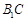 所成的角;
所成的角; ⊥平面
⊥平面 .
.
 中,
中,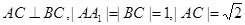 ,点M是
,点M是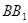 的中点,Q是AB的中点,
的中点,Q是AB的中点,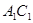 上的一动点,求证:
上的一动点,求证: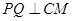 ;
;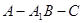 大小的余弦值.
大小的余弦值.