Question

5．已知函数f（x）=$\left\{{\begin{array}{l}{|{lg|x|}|，x≠0}\\{1，x=0}\end{array}}$，若关于x的方程f²（x）+af（x）+b=0有9个不同的实数根．   
（1）求a+b的值；    
（2）求a的取值范围．

Answer 1

分析 （1）令f（x）=t，根据f（x）的函数图象判断f（x）=t的解的个数，得出t=1为方程t²+at+b=0的解．
（2）当f（x）=t，t＞0且t≠1时，关于x的方程f²（x）+af（x）+b=0有9个不同实数解，据此即可求得实数a的取值范围．

解答 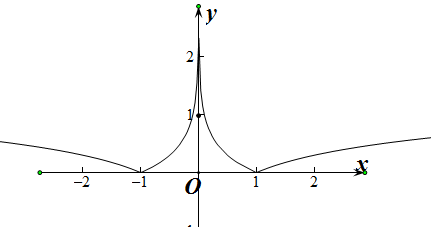解：（1）做出f（x）的函数图象如图所示：
设f（x）=t，则当t=1时，f（x）=t有5个解，当t≠1时，f（x）=t有4个解．
∵关于x的方程f²（x）+af（x）+b=0有9个不同的实数解，
∴关于t的方程t²+at+b=0有两解，且t=1是其中一解，
∴1+a+b=0，即a+b=-1．
（2）当f（x）=t，t＞0且t≠1时，关于x的方程f²（x）+af（x）+b=0有9个不同实数解，
∴t²+at-1-a=0，
∴a=-1-t，∵t＞0且t≠1，
∴a∈（-∞，-2）∪（-2，-1）

点评 本题考查了方程的根与函数图象的关系，数形结合是数学解题中常用的思想方法，能够变抽象思维为形象思维，有助于把握数学问题的本质；另外，由于使用了数形结合的方法，很多问题便迎刃而解，且解法简捷．属于中档题．