题目内容

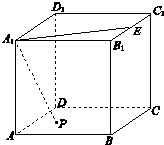（2013•西城区一模）如图，正方体ABCD-A1B1C1D1中，E是棱B1C1的中点，动点P在底面ABCD内，且PA1=A1E，则点P运动形成的图形是（　　）
分析：设正方体的棱长为1，求得PA1=A1E=
5
2
，求得AP=
PA12-AA12
=
1
2
，从而根据圆的定义以及题中条件得到点P运动形成的图形．
解答：解：正方体ABCD-A1B1C1D1中，E是棱B1C1的中点，动点P在底面ABCD内，且PA1=A1E，设正方体的棱长为1，
则且PA1=A1E=
A1B12+B1E2
=
1+
1
4
=
5
2
，∴AP=
PA12-AA12
=
1
2
．
故点P的轨迹是以A为圆心，以
1
2
为半径的圆弧（圆位于底面ABCD内的部分），
故选B．
点评：本题主要考查圆的定义，勾股定理的应用，求得 AP=
1
2
，是解题的关键，属于中档题．
练习册系列答案
相关题目
（2013•西城区一模）从甲、乙等5名志愿者中选出4名，分别从事A，B，C，D四项不同的工作，每人承担一项．若甲、乙二人均不能从事A工作，则不同的工作分配方案共有（　　）
（2013•西城区一模）某商区停车场临时停车按时段收费，收费标准为：每辆汽车一次停车不超过1小时收费6元，超过1小时的部分每小时收费8元（不足1小时的部分按1小时计算）．现有甲、乙二人在该商区临时停车，两人停车都不超过4小时．
（Ⅰ）若甲停车1小时以上且不超过2小时的概率为
1
3
，停车付费多于14元的概率为
5
12
，求甲停车付费恰为6元的概率；
（Ⅱ）若每人停车的时长在每个时段的可能性相同，求甲、乙二人停车付费之和为36元的概率．
（2013•西城区一模）设等比数列{an}的公比为q，前n项和为Sn，且a1＞0．若S2＞2a3，则q的取值范围是（　　）
（2013•西城区一模）记实数x1，x2，…，xn中的最大数为max{x1，x2，…，xn}，最小数为min{x1，x2，…，xn}．设△ABC的三边边长分别为a，b，c，且a≤b≤c，定义△ABC的倾斜度为t=max{
a
b
，
b
c
，
c
a
}•min{
a
b
，
b
c
，
c
a
}．
（ⅰ）若△ABC为等腰三角形，则t=
1
1
；
（ⅱ）设a=1，则t的取值范围是
[1，
1+
5
2
)
[1，
1+
5
2
)
．
（2013•西城区一模）如图，正六边形ABCDEF的边长为1，则
AC
•
DB
=
-
3
2
-
3
2
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网