题目内容
设奇函数f(x)在(0,+∞)上为单调递减函数,且f(2)=0,则不等式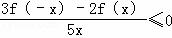 的解集为( )
的解集为( )
|
| A. | (﹣∞,﹣2]∪(0,2] | B. | [﹣2,0]∪[2,+∞) | C. | (﹣∞,﹣2]∪[2,+∞﹚ | D. | [﹣2,0)∪(0,2] |
D解:∵函数f(x)在(0,+∞)上为单调递减函数,且f(2)=0∴函数f(x)在(0,2)的函数值为正,在(2,+∞)上的函数值为负当x>0时,不等式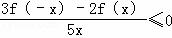 等价于3f(﹣x)﹣2f(x)≤0又奇函数f(x),所以有f(x)≥0所以有0<x≤2同理当x<0时,可解得﹣2≤x<0综上,不等式
等价于3f(﹣x)﹣2f(x)≤0又奇函数f(x),所以有f(x)≥0所以有0<x≤2同理当x<0时,可解得﹣2≤x<0综上,不等式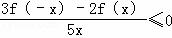 的解集为[﹣2,0)∪(0,2]故选D
的解集为[﹣2,0)∪(0,2]故选D

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
 的前
的前 项和为
项和为 且满足
且满足 则
则 中最大的项为 ( )
中最大的项为 ( )







 中,
中,  ,数列
,数列 是等比数列,且
是等比数列,且 ,则
,则 ( ) A.4 B.8 C.16 D.36
( ) A.4 B.8 C.16 D.36 是定义在实数集
是定义在实数集 上的不恒为零的偶函数,且对任意实数
上的不恒为零的偶函数,且对任意实数 都有
都有 ,则
,则 的值是( )
的值是( ) C.1 D.
C.1 D.
 ,且
,且 ,则
,则 的最小值是________.
的最小值是________.  .若
.若 ,且
,且 ,则
,则 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.
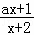 在区间(﹣2,+∞)上为增函数,则实数a的取值范围是 .
在区间(﹣2,+∞)上为增函数,则实数a的取值范围是 . ,
, 则
则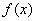 为( )
为( ) 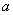 有关
有关  ,在
,在 上定义运算
上定义运算 :
: ,其中
,其中 为
为 被4除的余数,
被4除的余数, ,则使关系式
,则使关系式 成立的有序数对
成立的有序数对 的组数为 ( )
的组数为 ( ) B.
B. C.
C. D.
D.